Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

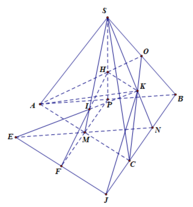
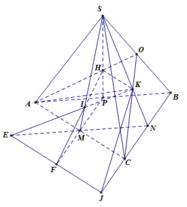
Gọi Q là trung điểm AB
Trong mp(IHS), gọi \(P=MQ\cap IH\)
a) Ta có:
\(\left\{{}\begin{matrix}P\in IH\subset\left(IHK\right)\\P\in MQ\subset\left(ABC\right)\end{matrix}\right.\)\(\Rightarrow P\in\left(IHK\right)\cap\left(ABC\right)\)
Lại có:
\(\left\{{}\begin{matrix}HK\text{/}\text{/}AC\left(Thales\right)\\HK\subset\left(IHK\right)\\AC\subset\left(ABC\right)\\\left(IHK\right)\cap\left(ABC\right)=d\end{matrix}\right.\)\(\Rightarrow d\text{/}\text{/}HK\text{/}\text{/}AC\)
\(\Rightarrow\left(IHK\right)\cap\left(ABC\right)=d\) đi qua P và \(d\text{/}\text{/}HK\text{/}\text{/}AC\)
b) Ta có:
\(\left\{{}\begin{matrix}S\in IM\subset\left(IHM\right)\\S\in\left(SBC\right)\end{matrix}\right.\)\(\Rightarrow S\in\left(IHM\right)\cap\left(SBC\right)\)
Lại có:
\(\left\{{}\begin{matrix}QM\text{/}\text{/}BC\left(Thales\right)\\QM\subset\left(IHM\right)\\BC\subset\left(SBC\right)\\\left(IHM\right)\cap\left(SBC\right)=d\text{'}\end{matrix}\right.\)\(\Rightarrow d\text{'}\text{/}\text{/}QM\text{/}\text{/}BC\)
\(\Rightarrow\left(IHM\right)\cap\left(SBC\right)=d\text{'}\) đi qua S và \(d\text{'}\text{/}\text{/}QM\text{/}\text{/}BC\)

a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
b: Xét (SAD) và (SBC) có
AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
d: Trong mp(SAB), gọi I là giao điểm của AB với SM
\(I\in SM;I\in AB\subset\left(ABCD\right)\)
Do đó: I là giao điểm của SM với mp(ABCD)

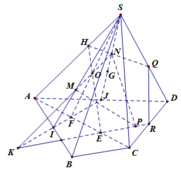
a) Ta có SM = MN = NA và G là trọng tâm của tam giác ABC. Khi đó, ta có:
SG = 2GM (vì G là trọng tâm)
SG = 2GN (vì G là trọng tâm)
Vậy GM = GN
Do đó, ta có tam giác SMN là tam giác đều.
Vì SM = MN = NA, nên tam giác SNA cũng là tam giác đều.
Từ đó, ta có góc SNA = 60°.
Mà góc SNA = góc SNB + góc BNA = góc SNB + góc BNC.
Vậy góc SNB + góc BNC = 60°.
Nhưng góc SNB + góc BNC = góc SBC.
Vậy góc SBC = 60°.
Do đó, GM // (SBC).
b) Gọi D là điểm đối xứng của A qua G.
Ta có GD = GA (vì D là điểm đối xứng của A qua G)
Và GM = GN (vì G là trọng tâm)
Vậy tam giác GDM và tam giác GAN là tam giác đồng dạng (cạnh bằng nhau và góc bằng nhau).
Từ đó, ta có góc GDM = góc GAN.
Nhưng góc GDM = góc MCD và góc GAN = góc NGB.
Vậy góc MCD = góc NGB.
Do đó, (MCD) // (NBG).
c) Gọi H = DM ∩ (SBC).
Ta cần chứng minh H là trọng tâm của tam giác SBC.
Vì G là trọng tâm của tam giác ABC, nên AG = 2GM.
Và GD = GA (vì D là điểm đối xứng của A qua G).
Từ đó, ta có AD = 2GD.
Vậy D là trọng tâm của tam giác AGD.
Do đó, DH là đường cao của tam giác AGD.
Vậy DH cắt AG tại I sao cho AI = 2IG.
Mà AI = 2IG nên I là trọng tâm của tam giác AGD.
Vậy I nằm trên đường thẳng DM.
Từ đó, ta có H = DM ∩ (SBC) là trọng tâm của tam giác SBC.
Vậy H là trọng tâm của tam giác SBC.

Hôm nay đi cắt lại cái kính, uay đi uay lại mất luôn buổi sáng :(

Bài này để sáng mai thử nghĩ coi sao nhó :) Giờ đi học hóa đã, rảnh inbox tui tán chuyện phiếm xí, dạo này ông anh đi làm đồ án chán chả có ai ngồi nói chuyện cùng :(