Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
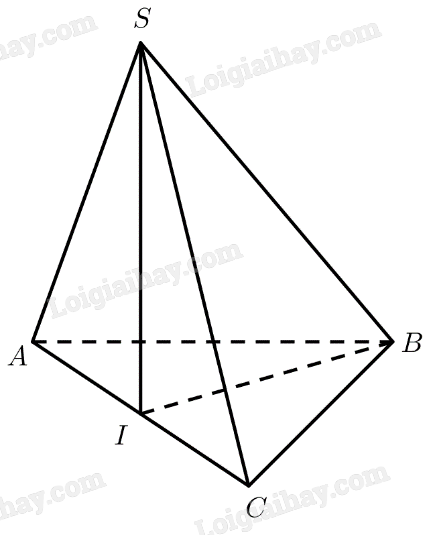
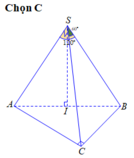
Xét tam giác \(SAC\) có:
\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}} = a\sqrt 3 \)
\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)
Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)
\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)
Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}} = a\sqrt 2 \)
Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy \(BC = a\)
Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)
\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)
Ta có:
\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)
Chọn D.
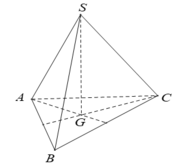
Cách 1:
- Ta có: SA = SB = SC nên:
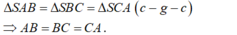
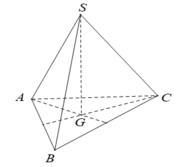
- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.
- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).
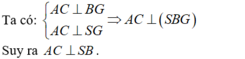
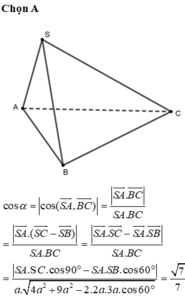
- Vậy góc giữa cặp vectơ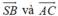 
bằng 90°.
Cách 2:
- Ta có:
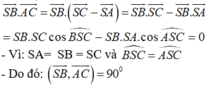
Chọn D.
Cách 1:
- Ta có: SA = SB = SC nên:
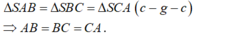
- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.
- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).
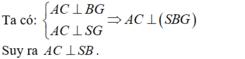
- Vậy góc giữa cặp vectơ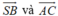 
bằng 90°.
Cách 2:
- Ta có:
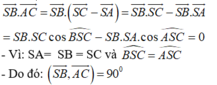
\(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\)
\(AC=\sqrt{SA^2+SC^2-2SA.SC.cos120^0}=\sqrt{3}\)
\(BC=\sqrt{SB^2+SC^2-2SB.SC.cos60^0}=a\)
\(\Rightarrow AB^2+BC^2=AC^2\Rightarrow\Delta ABC\) vuông tại B
Gọi H là hình chiếu vuông góc của S lên (ABC) \(\Rightarrow\) H là tâm đường tròn ngoại tiếp ABC (do SA=SB=SC)
\(\Rightarrow\) H trùng trung điểm AC
Gọi M là trung điểm SA \(\Rightarrow MH||SC\Rightarrow\) góc giữa SC và (SAB) bằng góc giữa MH và (SAB)
Gọi N là trung điểm AB \(\Rightarrow HN\perp AB\Rightarrow AB\perp\left(SHN\right)\)
Trong mp (SHN), kẻ \(HK\perp SN\Rightarrow HK\perp\left(SAB\right)\)
\(\Rightarrow\widehat{KMH}\) là góc giữa SC và (SAB)
\(SH=\sqrt{SA^2-\left(\dfrac{AC}{2}\right)^2}=...\)
\(MH=\dfrac{1}{2}SA=...\) (trung tuyến ứng với cạnh huyền)
\(NH=\dfrac{1}{2}BC=...\) (đường trung bình)
\(\Rightarrow\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}\Rightarrow HK=...\)
\(\Rightarrow sin\widehat{KMH}=\dfrac{HK}{MH}=...\)
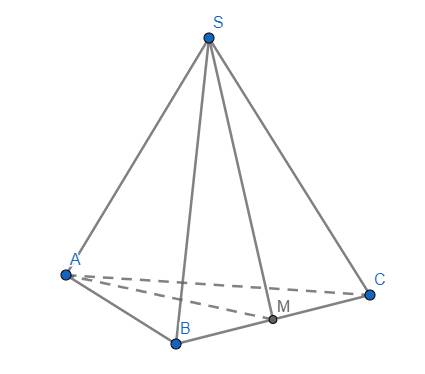
Theo đề bài, dễ có \(\Delta SAB=\Delta SBC=\Delta SCA\left(c.g.c\right)\)
\(\Rightarrow AB=BC=CA\)
Gọi M là trung điểm của BC. Khi đó \(\left\{{}\begin{matrix}SM\perp BC\\AM\perp BC\end{matrix}\right.\) (do các tam giác SBC và ABC lần lượt cân tại S và A). Suy ra \(BC\perp\left(SAM\right)\) \(\Rightarrow BC\perp SA\)
Hoàn toàn tương tự, ta có đpcm.
Đáp án D.
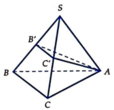
Gọi B', C' là trung điểm SB, SC. Thiết diện là ∆ AB'C'
Ta có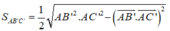 
Tương tự ta có 
Vậy 
