Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

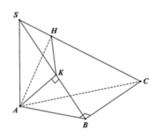
Chọn B
Phương pháp
Góc giữa đường thẳng và mặt phẳng (nhỏ hơn 90 o ) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Cách giải:
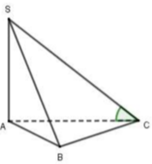
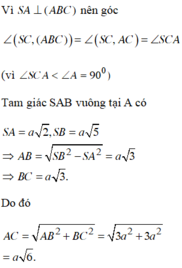
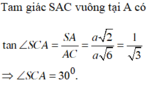

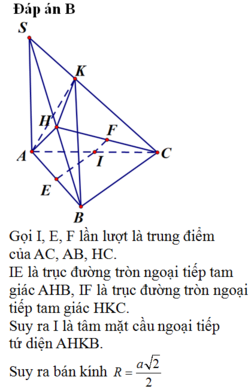
Đáp án B
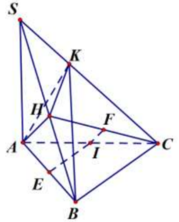
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
⇒ IA=IB=IC=IH=IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R= a 2 2

Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
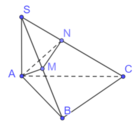
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 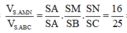
![]()
Do đó ![]()
![]()
Chọn C.

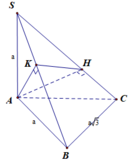
Đáp án C
Ta có
![]()
![]()
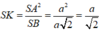
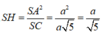
V S . A H K V S . A B C = S K . S H S B . S C = 1 10
⇒ V S . A H K = 1 10 V S . A B C = 1 60 3 a 3
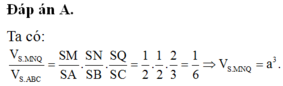
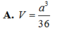
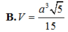

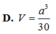
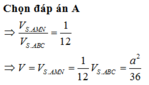
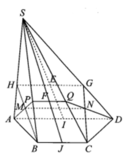
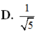

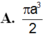
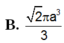

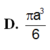
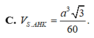


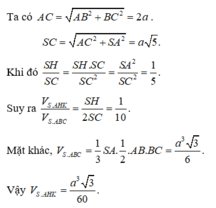
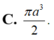
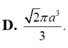


a. Tam giác ABC vuông cân tại A....Suy ra AB=AC=2a
\(Vs.abc=\dfrac{1}{3}.SA.S_{\Delta ABC}=\dfrac{1}{3}.a.\dfrac{1}{2}.2a.2a=\dfrac{2}{3}a^3\)
b. Tính S khối chóp bằng phương pháp tỉ số thể tích
Cho h/c S.ABC có mp \(\left(\alpha\right)\) không qua S cắt SA,SB,SC tại A',B',C', khi đó:
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
Cm: Kẻ C'H' , CH lần lượt vuông góc với SB', SB
\(\Rightarrow\dfrac{S_{SB'C'}}{S_{SBC}}=\dfrac{\dfrac{1}{2}.C'H'.SB'}{\dfrac{1}{2}CH.SB}=\dfrac{SC'}{SC}.\dfrac{SB'}{SB}\)
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{S_{SB'C'}.d\left(A',\left(SB'C'\right)\right)}{S_{SBC}.d\left(A,\left(SBC\right)\right)}\)
\(=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
Áp dụng: \(\dfrac{V_{SMNP}}{V_{SABC}}=\dfrac{3}{4}.\dfrac{4}{5}.\dfrac{5}{6}=\dfrac{1}{2}\)
\(\Rightarrow V_{MNPABC}=V_{SABC}-V_{SMNP}=\dfrac{1}{2}V_{SABC}=\dfrac{1}{3}a^3\)