Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Công thức
R = B C 2 sin B A C ⏜ = a 2 + 2 a 2 − 2 a . a 2 cos 45 ° 2 sin 45 ° = a 2 ⇒ V = 4 3 π R 3 = π a 3 2 3

Đáp án D
Phương pháp giải:
Xác định tâm mặt cầu ngoại tiếp đi qua các đỉnh của khối chóp bằng phương pháp dựng hình, từ đó dựa vào tính toán xác định bán kính – thể tích mặt cầu.
Lời giải:


Đáp án B
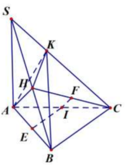
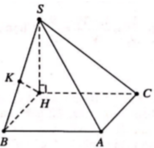
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
=> IA = IB = IC = IH = IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R = 2 π a 3 3

Đáp án B
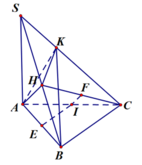
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC.
IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB. Suy ra bán kính R = a 2 2

Đáp án C
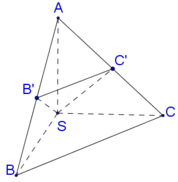
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
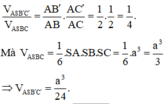

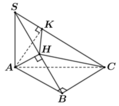
Theo giả thiết, ta có ![]() và
và ![]()
Do 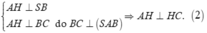
Từ (1) và (2) suy ra ba điểm B, H, K cùng nhìn xuống AC dưới một góc 90 ° nên
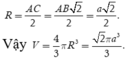
Chọn C.
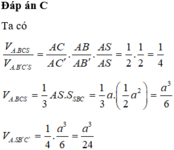



Đáp án A
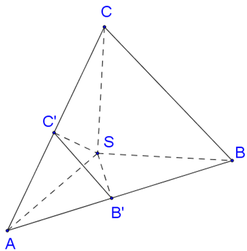
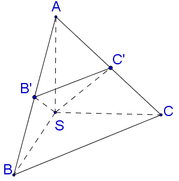
Dễ thấy Δ A B C là tam giác vuông cân tại B, do đó O A = O B = O C (với O là trung điểm của AC)
Ta có B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ A B 1 , lại do A B 1 ⊥ S B ⇒ A B 1 ⊥ B 1 C
Do đó Δ A B 1 C vuông tại O nên O A = O C = O B 1
Vậy O là tâm mặt cầu ngoại tiếp hình chóp A B C C 1 B 1
Do đó R = A C 2 = a 2 2 ⇒ V = 4 3 π R 3 = π a 3 2 3