Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
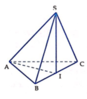
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do S A = S B = S C nên I A = I B = I C ⇒ I là tâm đường tròn ngoại tiếp Δ A B C . Mà Δ A B C vuông cân tại A nên I là trung điểm của BC và I A = I B = I C = 1 2 B C = a 2 2 .
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên S A , A B C ^ = S A , I A ^ = S A I ^ = 45 0 .
Do Δ S I A vuông tại I nên Δ S A I vuông cân tại I, khi đó : S I = I A = a 2 2 ⇒ d S ; A B C = S I = a 2 2

Đáp án B
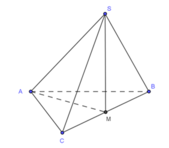
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của .
Ta có S A , A B C ^ = S A , A M ^ = S A M = 45 0
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của BC vì thế
A M = 1 2 B C = a 2 2
ta có
d S ; A B C = S M = A M . tan S A M = a 2 2 . tan 45 0 = a 2 2

Chọn C.
Phương pháp: Sử dụng công thức tính thể tích khối chóp khi biết ba góc ở một đỉnh và ba cạnh ở đỉnh đó.
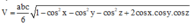
(trong đó a, b, c là độ dài ba cạnh, x, y, z là số đo ba góc ở một đỉnh)
Sau đó tính khoảng cách dựa vào công thức tính thể tích h = 3 V h .
Cách giải: Áp dụng công thức trên ta có:
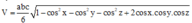
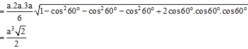


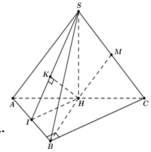
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Chọn B.
Phương pháp:
+ Gọi H là trung điểm BC. Ta chứng minh A H ⊥ A B C và AH là trục đường tròn ngoại tiếp tam giác
SBC
+ Suy ra tâm mặt cầu ngoại tiếp chóp S. ABC là giao của AH và đường trung trực cạnh AB.
+ Chỉ ra tam giác SBC vuông tại S từ đó tính SC theo định lý Pytago.
Cách giải:
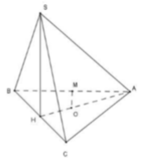




Ta chọn (SBC) làm mặt đáy => chiều cao khối chóp là d(A, (SBC)) = 3a
Tam giác SBC vuông cân tại S nên ![]()
Vậy thể tích khối chóp ![]()
Chọn A.
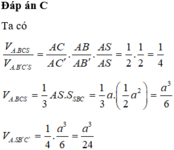
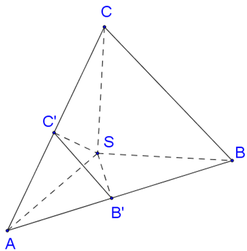
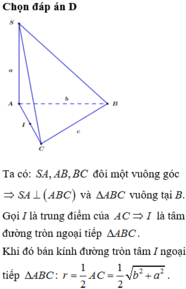

Đáp án D
Phương pháp:
- Gọi H là trực tâm tam giác, chứng minh S H ⊥ A B C bằng cách sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”.
- Tính độ dài SH bằng cách sử dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông.
Cách giải: Gọi H là trực tâm của tam giác ABC.
Ta sẽ chứng minh SH là đường cao của hình chóp.
Gọi E, D lần lượt là hình chiếu của B,A lên AC,BC.
Chú ý khi giải: Từ nay về sau, các em có thể ghi nhớ hệ thức liên hệ giữa đường cao và cạnh trong hình chóp S.ABC mà có SA, SB, SC đôi một vuông góc, đó là 1 S H 2 = 1 S A 2 1 S B 2 + 1 S C 2