K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2021
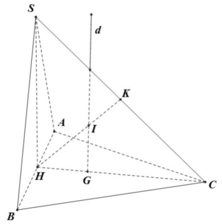
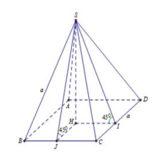
Gọi M là trung điểm SA và O là tâm đáy \(\Rightarrow AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AM=\dfrac{a}{2}\)
Qua O kẻ đường thẳng d song song SA, trong mặt phẳng (SAO) qua M kẻ đường thẳng song song AO cắt d tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(R=IA=\sqrt{IM^2+AM^2}=\sqrt{AO^2+AM^2}=\dfrac{a\sqrt{21}}{6}\)

NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 10 2021
\(\left\{{}\begin{matrix}CD\perp AD\left(gt\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D


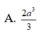
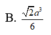





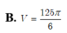


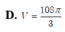
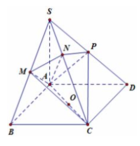

Lời giải:
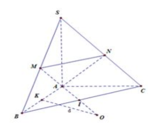
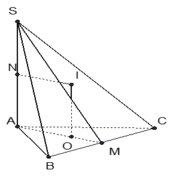
Kẻ \(SH\perp BC\). Ta thấy:
\(\left\{\begin{matrix} (SBC)\perp (ABC)\\ (SBC)\cap (ABC)\equiv BC\\ SH\perp BC\end{matrix}\right.\Rightarrow SH\perp (ABC)\)
Ta thấy giác $SBC$ và $ABC$ đều là tam giác vuông cân có cạnh huyền chung $BC$ nên $SB=SC=AB=a$
Bằng cách tính toán đơn giản, \(S_{ABC}=\frac{AB.AC}{2}=\frac{a^2}{2}\)
\(SH=\sqrt{\frac{SB^2.SC^2}{SB^2+SC^2}}=\frac{a}{\sqrt{2}}\)
\(\Rightarrow V_{S.ABC}=\frac{S_{ABC}.SH}{3}=\frac{a^3\sqrt{2}}{12}(\text{đvtt})\)