Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BP=\dfrac{1}{3}AB\Rightarrow BP=\dfrac{1}{2}AP\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}d\left(A;\left(SPC\right)\right)\)
Trong tam giác APC, kẻ \(AH\perp CP\Rightarrow CP\left(SAH\right)\)
Trong tam giác vuông SAH, kẻ \(AK\perp SH\Rightarrow AK\perp\left(SPC\right)\Rightarrow AK=d\left(A;\left(SPC\right)\right)\)
\(AP=\dfrac{2}{3}AB=\dfrac{2a}{3}\Rightarrow CP=\sqrt{AP^2+AC^2-2AP.AC.cos60^0}=\dfrac{a\sqrt{7}}{3}\)
Áp dụng định lý hàm sin:
\(\dfrac{AP}{sin\widehat{ACP}}=\dfrac{CP}{sinA}\Rightarrow sin\widehat{ACP}=\dfrac{AP.sin60^0}{CP}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow AH=AC.sin\widehat{ACP}=\dfrac{a\sqrt{21}}{7}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{2a\sqrt{93}}{31}\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}AK=\dfrac{a\sqrt{93}}{31}\)
Bạn kiểm tra lại phần tính toán


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=

Chọn A
Xác định được
![]()
![]()
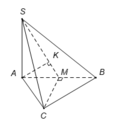
Do M là trung điểm của cạnh AB nên
![]()
![]()
![]()
Tam giác vuông SAM có
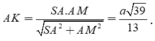
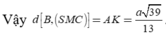

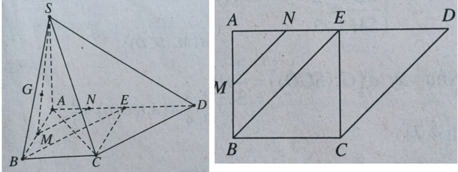
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).

Gọi K là trung điểm của SA
=>KM//SC
=>SC//(KMB)
d(SC;BM)=d(S;(KBM))=SK/SA*d(A;(KBM))=d(A;(KBM))
=>ΔABC đều
=>BM vuông góc AC
=>BM vuông góc (SAC)
Kẻ AQ vuông góc KM
=>AQ vuông góc (KMB)
=>d(A;(KMB))=AQ
\(SC=\sqrt{9a^2+4a^2}=a\sqrt{13}\)
KM=1/2SC=a*căn 3/2
=>\(AQ=\dfrac{3\sqrt{13}}{13}\)
=>d(BM;SC)=3*căn 13/13

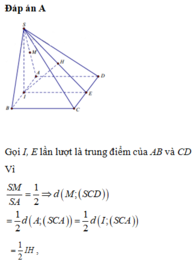


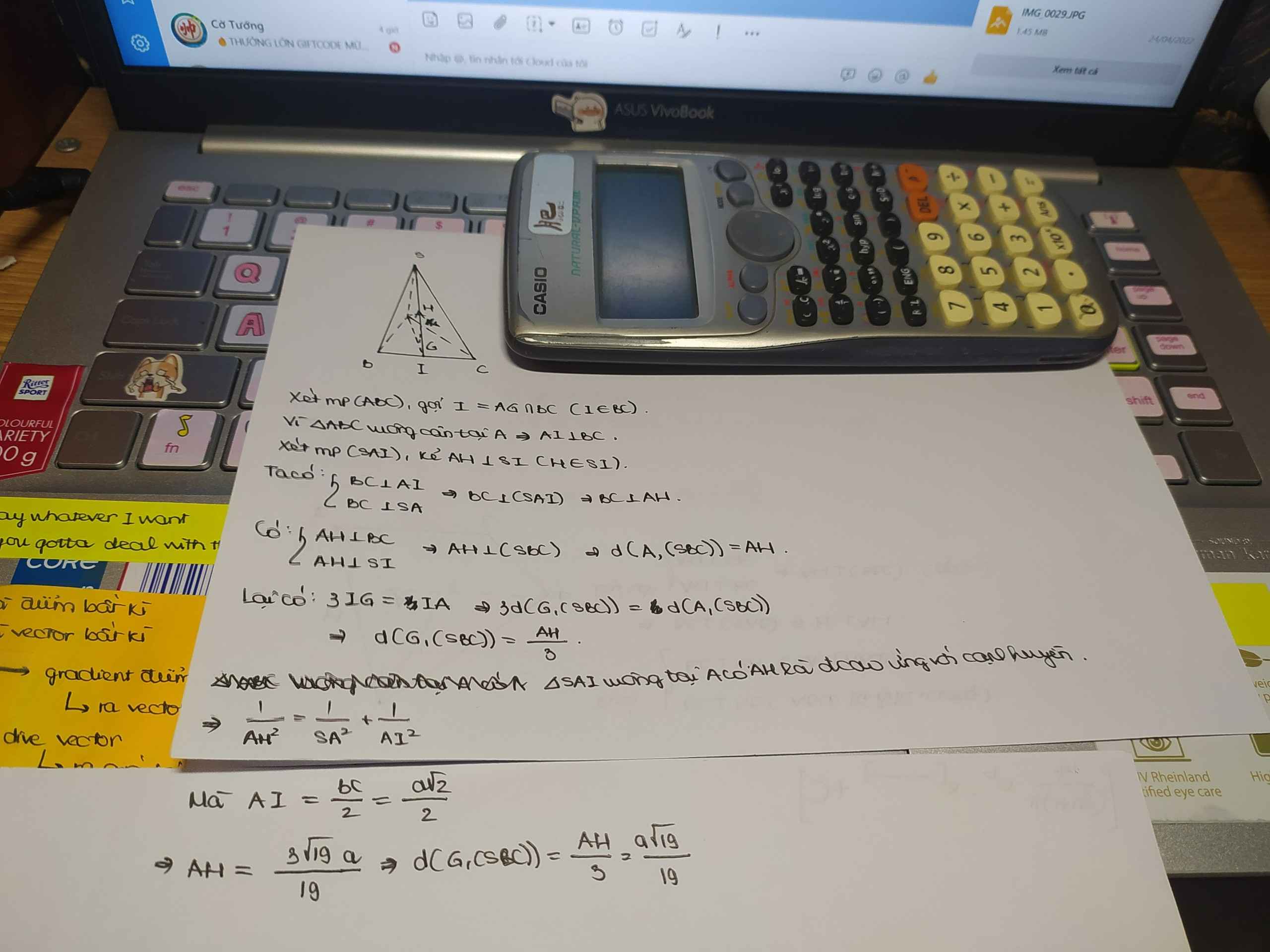
Đề bài thiếu và sai rất nhiều
1. SA có liên hệ gì với đáy?
2. Đáy là tam giác đều cạnh dài bao nhiêu
3. B thuộc (SBP) nên hiển nhiên khoảng cách từ B đến (SBP) bằng 0, không cần phải tính
em sửa r ạ