Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải: Gọi H là trung điểm của AC
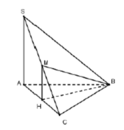
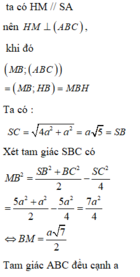
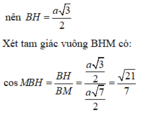

Đáp án B
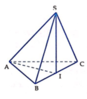
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do S A = S B = S C nên I A = I B = I C ⇒ I là tâm đường tròn ngoại tiếp Δ A B C . Mà Δ A B C vuông cân tại A nên I là trung điểm của BC và I A = I B = I C = 1 2 B C = a 2 2 .
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên S A , A B C ^ = S A , I A ^ = S A I ^ = 45 0 .
Do Δ S I A vuông tại I nên Δ S A I vuông cân tại I, khi đó : S I = I A = a 2 2 ⇒ d S ; A B C = S I = a 2 2

Đáp án B.
Gọi H là hình chiếu vuông góc của S trên (ABC)
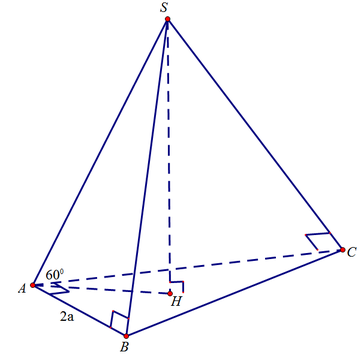
Ta có A C ⊥ S H C ⇒ A C ⊥ H C ⇒ H C / / A B .
Tương tự A B ⊥ S H B ⇒ A B ⊥ H B ⇒ H B / / A C
Vậy H là đỉnh thứ tư của hình vuông BACH như hình vẽ sau:
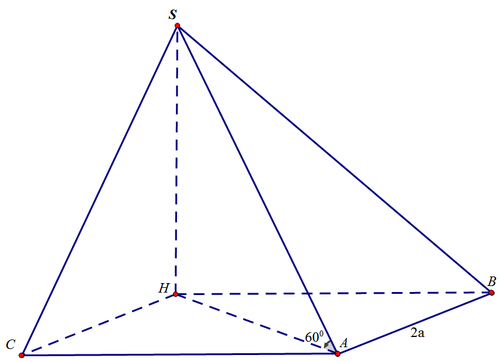
Khi ấy, ta có: A H = 2 a 2 ⇒ S H = 2 a 6
⇒ V S . A B H C = 1 3 S H . S A B H C = 1 3 2 a 6 .4 a 2 = 8 6 a 3 3
⇒ V S . A B C = 1 2 V S . A B H C = 4 6 a 3 3



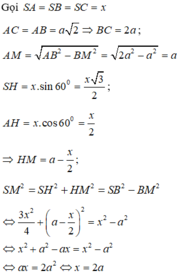

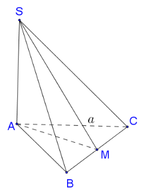

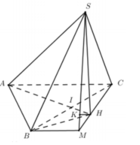



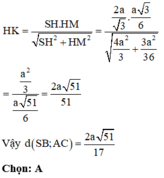

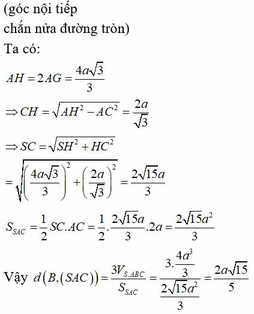
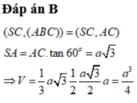
Đáp án A
Phương pháp:
- Xác định góc giữa đường thẳng AB và mặt phẳng (P):
Bước 1: Xác định giao điểm I của AB và (P)
Bước 2: Từ B hạ BH vuông góc với (P)
Bước 3: Nối IH => Góc HIB là góc tạo bởi AB và (P).
Cách giải:
Gọi D là trung điểm của AB.
Tam giác ABC đều => CD ⊥ AB
Mà CD ⊥ SA, do SA ⊥ (ABC)
=> CD ⊥ (SAB) => (SC, (SAB)) = (SC, SD) = CSD
Tam giác ABC đều, cạnh a, M là trung điểm AB
Tam giác ADS vuông tại A
Tam giác SDC vuông tại D