Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)

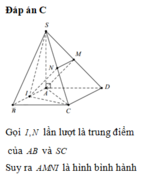
Gọi N, Q lần lượt là trung điểm của AB , CD \(\Rightarrow\left\{{}\begin{matrix}MN\perp AB\\MQ\perp AB\end{matrix}\right.\)
Qua N kẻ đường thẳng song song với BC , cắt SC tại P
suy ra thiết diện của mặt phẳng (\(\alpha\) ) và hình chóp là MNPQ
Vì MQ là đường t/b của hình thang ABCD , \(\Rightarrow MQ=\dfrac{3a}{2}\)
MN là đường t/b của tam giác SAB; \(MN=\dfrac{SA}{2}=a\)
NP là đường t/b của tam giác SBC ; \(\Rightarrow NP=\dfrac{BC}{2}=\dfrac{a}{2}\)
Vậy diện tích hình thang MNPQ là : \(S_{MNPQ}=\dfrac{MN.\left(NP+MQ\right)}{2}=\dfrac{a}{2}.\left(\dfrac{a}{2}+\dfrac{3a}{2}\right)=a^2\)

1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)

Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
b. \(\left\{{}\begin{matrix}SA\perp BD\\BD\perp SC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow\widehat{BCA}=\widehat{ABD}\) (góc có cạnh tương ứng vuông góc)
\(\Rightarrow AD=AB.tan\widehat{ABD}=AB.\dfrac{AB}{BC}=\dfrac{a}{2}\)
c. Theo c/m câu a ta có \(BC\perp\left(SAB\right)\), mà \(AD||BC\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp BM\)
Mà \(BM\perp DE\) (do DE là đường cao ứng với BM)
\(\Rightarrow BM\perp\left(ADE\right)\Rightarrow BM\perp AE\)
Áp dụng hệ thức lượng trong tam giác vuông ABM:
\(AE=\dfrac{AM.AB}{\sqrt{AM^2+AB^2}}=\dfrac{ax}{\sqrt{a^2+x^2}}\)
Pitago tam giác vuông ADE:
\(DE^2=AE^2+AD^2=\dfrac{a^2x^2}{a^2+x^2}+\dfrac{a^2}{4}\)
Do \(AD=\dfrac{a}{2}\) không đổi nên DE max, min tương ứng khi AE max, min
Hiển nhiên \(AE\ge0\Rightarrow AE_{min}=0\) khi \(x=0\) khi đó DE min
\(AE^2=\dfrac{a^2x^2}{a^2+x^2}\le\dfrac{a^2x^2}{2ax}=\dfrac{ax}{2}\le\dfrac{a^2}{2}\)
\(\Rightarrow AE_{max}\) khi \(x=3\)