Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

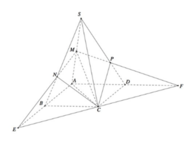
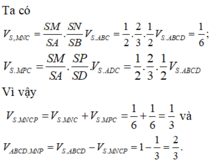
Cách 2: Dùng công thức tính nhanh tỷ số thể tích
Có
![]()
![]()
Vì Vậy
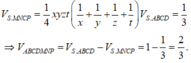

có
Gắn vào hệ trục Oxyz có
CÓ : S(0,0,0) A(0,0,a) , B(0,a,0), C(a,0,0)
e nhớ ko lầm là a đã học tới bài này âu mà sao bik làm hay z???

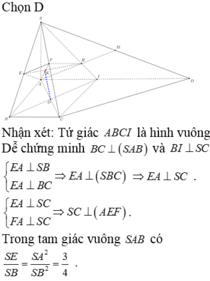
Chọn D
Thể tích khối chóp S. ABCD là:
![]()
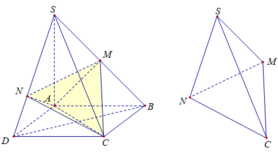
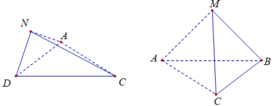
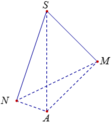
Thể tích tứ diện SMNC là:
![]() .
.
Thể tích tứ diện NACD là:
![]() .
.
Thể tích tứ diện MABC là:
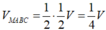 .
.
Thể tích tứ diện SAMN là:
![]() .
.
Mặt khác ta có:
![]()
Suy ra:
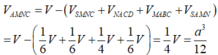

Phương pháp:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
(Công thức Simson): Cho khối chóp S.ABC, các điểm A1, B1, C1 lần lượt
thuộc SA, SB, SC. Khi đó,
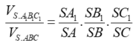
Cách giải:
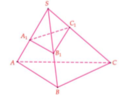
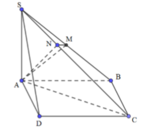
ABCD là hình chữ nhật ![]()
Ta có:
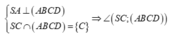
![]()
![]()
Thể tích khối chóp S.ABCD là:
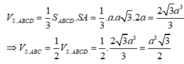
Ta có: 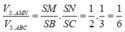
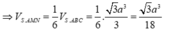
Chọn: B
Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng cho chóp tam giác.

Chắc là mp (P) đi qua A'
Đặt \(V_{SABCD}=V\)
Theo định lý Talet: \(\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{SD'}{SD}=\dfrac{3}{4}\)
Ta có: \(\dfrac{V_{SA'B'C'D'}}{V_{SABCD}}=\dfrac{2V_{SA'B'C'}}{2V_{SABC}}=\dfrac{V_{SA'B'C'}}{V_{SABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=\dfrac{3}{4}.\dfrac{3}{4}.\dfrac{3}{4}=\dfrac{27}{64}\)
Tỉ số thể tích 2 phần (phần trên chia phần dưới) là: \(\dfrac{27}{64}:\left(1-\dfrac{27}{64}\right)=\dfrac{27}{37}\)
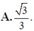



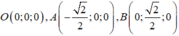
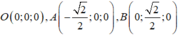
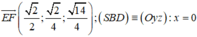
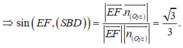
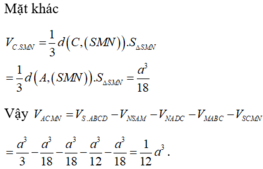
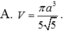
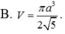
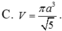


Vì \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB \Rightarrow \frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\left( { = \frac{1}{3}} \right)\)
Tam giác SAB có: \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\) nên FE//AB và \(EF = \frac{1}{3}AB\).
Vì hai vectơ \(\overrightarrow {EF} \) và \(\overrightarrow {AB} \) cùng hướng nên \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AB} \) (1)
Vì ABCD là hình bình hành nên \(AB = CD\) và AB//CD. Do đó, \(\overrightarrow {AB} = \overrightarrow {DC} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \)