Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
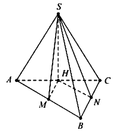
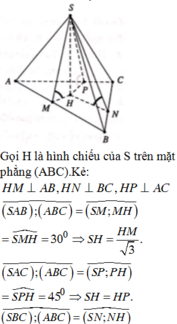
Gọi H là hình chiếu của S trên A C ⇒ S H ⊥ A B C
Kẻ H M ⊥ A B M ∈ A B , H N ⊥ A C N ∈ A C
Suy ra S A B ; A B C ^ = S B C ; A B C ^ = S M H ^ = S N H ^ = 60 °
⇒ ∆ S H M = ∆ S H N ⇒ H M = H N ⇒ H là trung điểm của AC
Tam giác SHM vuông tại H, có tan S M H ^ = S H H M ⇒ S H = a 3 2
Diện tích tam giác ABC là S ∆ A B C = 1 2 . A B . B C = a 2 2
Vậy thể tích cần tính là V = 1 3 . S H . S A B C = 1 3 . a 3 2 . a 2 2 = a 3 3 12

Đáp án B
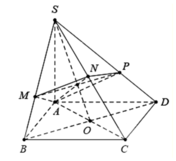
Nối S O ∩ A N = E , qua E kẻ đường thẳng song song với BD. Cắt SB,SD lần lượt tại M , P ⇒ m p P ≡ A M N P .
Ta có S A ⊥ A B , S A ⊥ A D ⇒ S A ⊥ A B C D ⇒ B C ⊥ S A B .
Mà SC ⊥ A M N P ⇒ S C ⊥ A M suy ra A M ⊥ S B C .
Do đó A M ⊥ M C mà O là trung điểm của A C ⇒ O A = O M = O C .
Tương tự, ta chứng minh được O là tâm mặt cầu ngoại tiếp khối
đa diện A B C D . M N P ⇒ R = A C 2 = 4 a 3 2 = 2 a 3 .
Vậy thể tích cần tính là V = 4 3 π R 3 = 4 3 π 2 3 3 = 32 3 π a 3 .
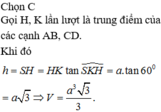

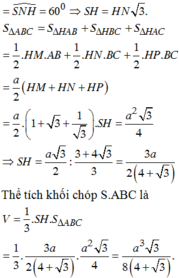


Đáp án D.
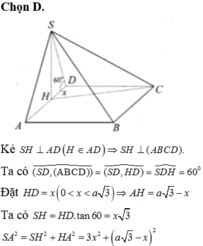
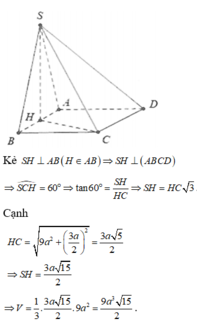
Gọi H là trung điểm của AB thì S H ⊥ A B C D ⇒ S H = a 2 .
Khoảng cách từ H đến BC, CD, DA đều là a 2 3 ⇒ S A B C D = 1 2 . a 2 3 . 9 a − a = 2 a 2 3 .
Vậy thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 2 . 2 a 2 3 = a 3 3 9 .