Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
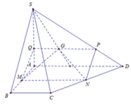
Do M N / / A D nên giao tuyến của (SAD) và (GMN) song song với AD
Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P
Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do đó thiết diện là hình bình hành

Đáp án A
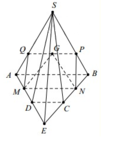
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB
Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.
Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Vì MN//PQ suy ra MNPQ là hình thang
Để MNPQ là hình bình hành ⇔ MN=PQ (1)
Gọi I là trung điểm của AB, G là trọng tâm tam giác S A B ⇒ S G S I = 2 3
Tam giác SAB có P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)
Mà MN là đường trung bình hình thang A B C D ⇒ M N = A B + C D 2 (3)
Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .

làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m
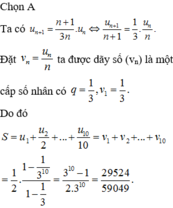
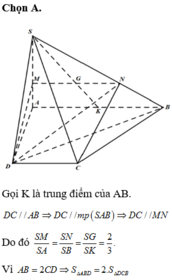

Đáp án A
Do M N / / A D nên giao tuyến của S A D và G M N song song với AD. Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P. Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do thiết diện là hình bình hành