Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

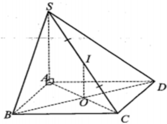
Gọi \(I\) là tâm của đáy \(ABCD\) (giao điểm của \(AC\) và \(BD\))
a) Vì đây là hính chóp đều nên có ngay \(SI\) là đường cao kẻ từ S
\(SI=\sqrt{SA^2-AI^2}=\sqrt{SA^2-\frac{AB^2}{2}}=a\sqrt{2}\)
\(V_{S.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{4a^3\sqrt{2}}{3}\)
b) Thấy ngay \(IA=IB=IC=ID=IS=a\sqrt{2}\)
suy ra tâm mc ngoại tiếp là \(I\) và \(R=a\sqrt{2}\)
c) bạn dùng công thức sau để tính bán kính mặt cầu nội tiếp
\(r=\frac{3V_{S.ABCD}}{S_{ABCD}+4S_{SAB}}=\frac{\frac{4a^3\sqrt{2}}{3}}{4a^2+4.\frac{a^2\sqrt{3}}{2}}=\frac{4\sqrt{2}-2\sqrt{6}}{3}.a\)

\(AC=2a\sqrt{2}.\sqrt{2}=4a\Rightarrow OA=\dfrac{1}{2}AC=2a\)
\(\Rightarrow SO=\sqrt{SA^2-OA^2}=2a\sqrt{3}\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{4a\sqrt{3}}{3}\)
\(\Rightarrow V=\dfrac{4}{3}\pi R^3=...\)

\(AC=2a\sqrt{2}.\sqrt{2}=4a\) \(\Rightarrow OA=\dfrac{1}{2}AC=2a\)
\(\widehat{SAO}=30^0\Rightarrow\left\{{}\begin{matrix}SO=AO.tan30^0=\dfrac{2a\sqrt{3}}{3}\\SA=\dfrac{AO}{cos30^0}=\dfrac{4a\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{4a\sqrt{3}}{3}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{256\pi a^3\sqrt{3}}{27}\)

Gọi M là trung điểm AB \(\Rightarrow\widehat{SMO}=45^0\)
\(OM=\dfrac{1}{2}AB=a\sqrt{2}\)
\(SO=OM.tan45^0=a\sqrt{2}\)
\(OA=\dfrac{1}{2}AC=2a\)
\(\Rightarrow SA=\sqrt{SO^2+OA^2}=a\sqrt{6}\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{3a\sqrt{2}}{2}\)
\(V=\dfrac{4}{3}\pi R^3=9\sqrt{2}\pi a^3\)