

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



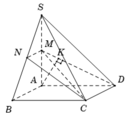
Xác định được ![]()
Vì M là trung điểm SA nên
![]()
Kẻ ![]() và chứng minh được
và chứng minh được ![]() nên
nên ![]()
Trong
∆
vuông MAD tính được ![]()
Chọn A.

Đáp án C
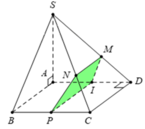
Kẻ I M ⊥ S D tại M Đường thẳng I M ⊂ m p P
ABCD là hình vuông ⇒ C D ⊥ A D mà S A ⊥ C D ⇒ C D ⊥ S A D
Ta có P ⊥ A D mà C D ⊥ A D ⇒ C D / / m p P
Qua I kẻ đường thẳng song song với CD, cắt BC tại P
Qua M kẻ đường thẳng song song với CD, cắt SC tại N
Suy ra mặt phẳng (P) cắt khối chóp S.ABCD theo thiết diện là hình thang vuông IMNP tại M và I.
Tam giác SAD vuông tại A có d A ; S D = a 3 ⇒ I M = a 3 2
Tam giác IMD vuông tại M có M D = I D 2 − I M 2 = a 2 ⇒ S M S D = 7 8 ⇒ M N = 7 a 4
Vậy diện tích hình thang IMNP là S = I M . M N + I P 2 = a 3 2 . 1 2 . 7 a 4 + 2 a = 15 3 16 a 2

Đáp án C.
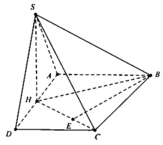
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .