Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra S I ⊥ ( A B C )
Gọi M là trung điểm của BC
Diện tích tam giác ABC là: ![]()
Vậy thể tích khối chóp ![]()
Chọn C.

\(A=\left(1-\frac{1}{1+2}\right)\left(1-\frac{1}{1+2+3}\right)...\left(1-\frac{1}{1+2+3+...+2006}\right)\)
\(A=\left(1-\frac{1}{\frac{\left(1+2\right).2}{2}}\right)\left(1-\frac{1}{\frac{\left(1+3\right).3}{2}}\right)...\left(1-\frac{1}{\frac{\left(1+2006\right).2006}{2}}\right)\)
\(A=\frac{2}{3}.\frac{5}{6}.\frac{9}{10}...\frac{2007.2006-2}{2006.2007}=\frac{4}{6}.\frac{10}{12}.\frac{18}{20}....\frac{2007.2006-2}{2006.2007}\) (1)
xét thấy:2007.2006-2=2006.(2008-1)+2006-2008=2006.(2008-1+1)-2008=2008.(2006-1)=2008.2005 (2)
(1),(2)\(=>A=\frac{4.1}{2.3}.\frac{5.2}{3.4}.\frac{6.3}{4.5}....\frac{2008.2005}{2006.2007}\)
\(A=\frac{\left(4.5.6...2008\right)\left(1.2.3...2005\right)}{\left(2.3.4....2006\right)\left(3.4.5...2007\right)}=\frac{2008}{2006.3}=\frac{1004}{3009}\)
Vậy A=1004/3009

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Chọn B.
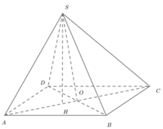
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.




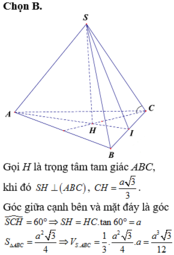
Chọn D.