Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

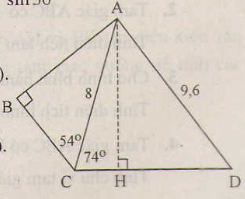
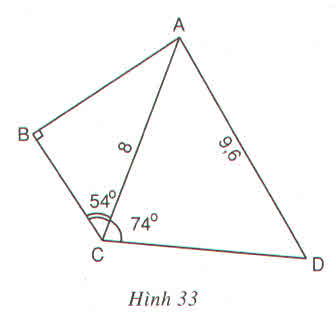
a) Xét tam giác ABC vuông tại B có: AB=AC.sinC=8.sin540≈6,472(cm)AB=AC.sinC=8.sin540≈6,472(cm)
b) Vẽ CD. Xét tam giác ACH có: AH=AC.sinC=8.sin740≈7,690(cm)AH=AC.sinC=8.sin740≈7,690(cm)
Xét tam giác AHD vuông tại H có: sinD=AHAD≈7,6909,6≈0,8010⇒ˆD=530sinD=AHAD≈7,6909,6≈0,8010⇒D^=530
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.

Chọn phương án (B)
Tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. Khi đó \(\widehat{BOC}\) có số đo bằng \(120^0\)

Chọn phương án (B)
Hình vuông XYZT nội tiếp đường tròn tâm O bán kính R. Điểm M bất kì thuộc cung XT. \(\widehat{ZMT}\) có số đo bằng \(45^0\)




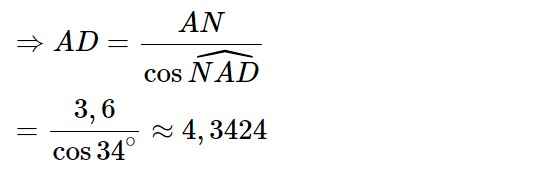

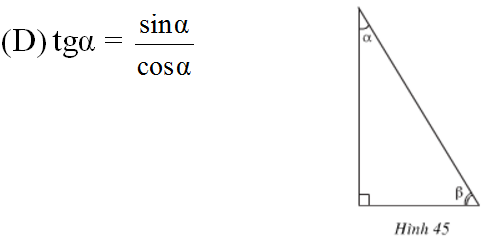
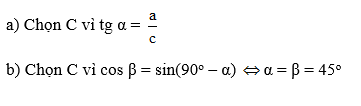

Chọn phương án (A)
Theo hình bS9, khi đó số đo của \(\widehat{MFE}\) bằng \(50^0\)