PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
9 tháng 10 2019
TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt
TM
5
21 tháng 11 2017
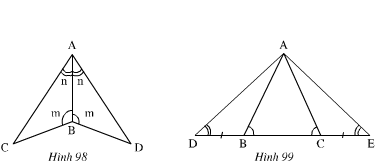
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
TH
21 tháng 11 2017
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
TT
1
1 tháng 5 2019
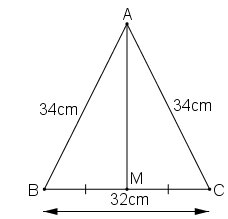
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).
6 tháng 11 2016
Bài 1:
a)\(\frac{2}{3}.\frac{5}{2}-\frac{3}{4}.\frac{2}{3}=\frac{5}{3}-\frac{1}{2}=\frac{7}{6}\)
b)\(2.\left(\frac{-3}{2}\right)^2-\frac{7}{2}=\frac{2.9}{4}-\frac{7}{2}=\frac{9-7}{2}=\frac{2}{2}=1\)
c)\(-\frac{3}{4}.\frac{68}{13}-0,75.\frac{36}{13}=\frac{-3.4.17}{4.13}-\frac{3.9.4}{4.13}=\frac{-51-27}{13}=\frac{-78}{13}=-6\)
Bài 2:
a)|x-1,4|=1,6
\(\Rightarrow\left[\begin{array}{nghiempt}x-1,4=1,6\\x-1,4=-1,6\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=3\\x=-0,2\end{array}\right.\)
b) \(\frac{3}{4}-x=\frac{4}{5}\)
\(x=\frac{3}{4}-\frac{4}{5}=-\frac{1}{20}\)
c)(1-2x)3=-8
(1-2x)3=(-2)3
1-2x=-2
2x=3
x=\(\frac{3}{2}\)
Bài 3:
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{7}=k\)
\(\Rightarrow\begin{cases}x=2k\\y=5k\\z=7k\end{cases}\)
A=\(\frac{2k-5k+7k}{2k+2.5k-7k}=\frac{4k}{5k}=\frac{4}{5}\)
=> x=4/5 . 2= 8/5
y=4/5 . 5=4
z=4/5.7=28/5
TT
3
NK
29 tháng 11 2016
0,2(63)= \(\frac{1}{10}\).[2+0,(63)] = \(\frac{1}{10}\).[2+0,(01).63] = \(\frac{1}{10}\).[2+\(\frac{1}{99}\).63] = \(\frac{1}{10}\).\(\frac{29}{11}\)=\(\frac{29}{110}\)
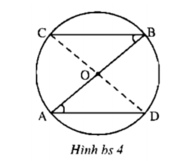
+) Xét tam giác OAD có: OA = OD (= bán kính đường tròn)
Suy ra tam giác OAD cân tại O.
Suy ra: ∠A = ∠D ( tính chất tam giác cân). (1)
+) Xét tam giác OBC có: OB = OC (= bán kính đường tròn)
Suy ra tam giác OBC cân tại O.
Suy ra: ∠B = ∠C ( tính chất tam giác cân). (2)
+) Lại có: ∠A = ∠B ( giả thiết) (3)
Từ (1); (2) và (3) suy ra: ∠A = ∠B = ∠C = ∠D
Vậy hai tam giác cân OAD và OBC có góc ở đáy bằng nhau nên góc ở đỉnh bằng nhau: ∠AOD = ∠BOC (4).
+) Ta có: ∠AOD + ∠DOB = 180º ( hai góc kề bù) (5)
Từ (4) và (5) suy ra: ∠BOC + ∠DOB = 180º hay 3 điểm C, O và D thẳng hàng.