Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : AB=CD (T/c HBH) mà K là TĐ của AB (gt) và I là TĐ của DC (gt)
Suy ra AK=KB=IC=ID (1) mà K thuộc AB, I thuộc DC nên AK// IC(2)
từ (1) (2) suy ra AKIC là HBH (dhnb) suy ra AI//KC(t/c)(đpcm) mà M thuộc AI, N thuộc KC suy ra AM//KN và MI//NC
b) xét tam giác DNC có: I là TĐ của DC và MI//NC(cmt) suy ra M là TĐ của DN(3)
CMTT suy ra N là TĐ của MB(4)
TỪ (3)(4) suy ra DM=MN=NB(ddpcm)

Giải :
a) + K là trung điểm của AB ⇒ AK = \(\frac{AB}{2}\).
+ I là trung điểm của CD ⇒ CI = \(\frac{CD}{2}\).
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = \(\frac{CD}{2}\) hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI // KC hay \(\frac{MI}{NC}\).
\(a)\)
\(K\)là trung điểm \(AB\)\(\Rightarrow AK=\frac{AB}{2}\)
\(I\)là trung điểm \(CD\)\(\Rightarrow CI=\frac{CD}{2}\)
Mà theo đề ra: \(ABCD\)là hình bình hành
\(\Rightarrow AB//CD\)hay \(AK//CI\)
\(\Rightarrow AB=CD\Rightarrow\frac{AB}{2}=\frac{CD}{2}\)hay \(AK=CI\)
Tứ giác \(AKCI\)có \(AK//CI\)\(;\)\(AK=CI\)
\(\Rightarrow AKCI\)là hình bình hành
\(b)\)
Theo phần a), ta có: \(AKCI\)là hình bình hành
\(\Rightarrow AI//KC\)hay \(MI//NC\)
A K B N M I C D

a ) AK = 1/2 AB
CI = 1/2 CD
Mà AB //= CD nên AK //= CI suy ra
AKCI - hình bình hành
Nên AI // CK
b ) Xét t/g DNC có :
I là trung điểm CD mà IM // NC
=> IM là đường trung bình của t/g DNC
=> MD = MN ( 1 )
Xét t/g ABM có :
K là trung điểm AB mà KN // AM
=> KN là đường trung bình của t/g ABM ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra DM = MN = NB

a,ta có:tg ABCD là hình bình hành
AB song song DC
AK song song IC (1)
mà K là trung điểm của AB
AK=1/2AB
tương tự IK=1/2DC
mà AB=DC
AK=IC (2)
từ (1)và(2)suy ra tg AKCI là hbh
AI song song KC
Chỉ giải được 1 câu thôi thông cảm nhé
câu b:
Vì AI//KC=)IM//NC.Tam giác DNC có đoạn IM cắt trung điểm của DC và // với NC=)M là trung điểm DN=)DM=MN
làm tương tự với tam giác AMB
chỉ giải được câu 2 thôi thông cảm nhé

a)Xét hbh ABCD có:
AB//CD, AB=Cd(t/c)
K là tđ AB
I là tđ CD
=> AK=IC, AK//IC
=> AKCI là hbh(dhnb)
=> AI//KC(t/c)
b) Xét tam giác ABM:
K là tđ AB
KN//AM(M thuộc AI, N thuộc KC)
=> KN là đg tb
=> MN=MB (t/c) (1)
Xét t.giác DNC
I là tđ CD
IM//NC
=> IM là đg tb của t.giác DNC
=> MD=MN (t/c) (2)
(1),(2)=> DM= MN= NB

Ta có hình vẽ: A K B C I D M N
a) Ta có: AK = \(\dfrac{1}{2}\) AB
IC = \(\dfrac{1}{2}\) DC
mà AB = DC (vì ABCD là hình bình hành)
=> AK = IC
=> AK // IC (vì AB // DC)
=> AKCI là hình bình hành
=> AI // KC
b) Xét \(\Delta ABM\) có:
AK = KB (gt)
AM // KN (vì AI // KC)
=> BN = MN (1)
Xét \(\Delta DNC\) có:
DI = IC (gt)
IM // CN (vì AI // KC)
=> DM = MN (2)
từ (1) và (2) => DM = MN =NB

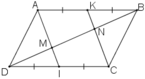
Cho hình bình hành ABCD. Gọi I,K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB

a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.


a)
Vì \(DC=AB\)(vì ABCD là hình bình hành) (1)
mà \(IC=ID\) (2)
\(KA=KB\)(3)
Từ (1) ;/ (2) và (3)
\(\Rightarrow IC=KB\)
Vì ABCD là hình b/hành
\(\Rightarrow AD=BC\)
và \(\widehat{ADI}=\widehat{CBK}\)
Xét \(\Delta ADI\)và \(\Delta CBK\)có :
\(AD=BC\left(cmt\right)\)
\(\widehat{ADI}=\widehat{CBK}\left(cmt\right)\)
\(DI=BK\)(cmt )
Do đó : \(\Delta ADI=\Delta CBK\)(c-g-c)
\(\Rightarrow\hept{\begin{cases}AI=CK\\\widehat{DAI}=\widehat{BCK}\end{cases}}\)
Mà \(\widehat{DAB}=\widehat{DCB}\)( vì ABCD Là hình bình hành )
\(\Rightarrow\widehat{IAB}=\widehat{ICK}\)
Mà hai góc này ở vị trí so le
\(\Rightarrow AI//CK\)
b) Xét \(\Delta MAB\)có :
\(KA=KB\left(gt\right)\)
và \(AM//KN\)(vì AI // KC )
=> MN= NB ( 1)
Xét \(\Delta CDN\)có :
\(ID=IC\left(gt\right)\)
và \(IM//CN\)(vì IA // CK )
=> DM = MN (2)
Từ (1) và (2)
\(\Rightarrow DM=MN=NB\)( đpcm)
A B C D K I M N