Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

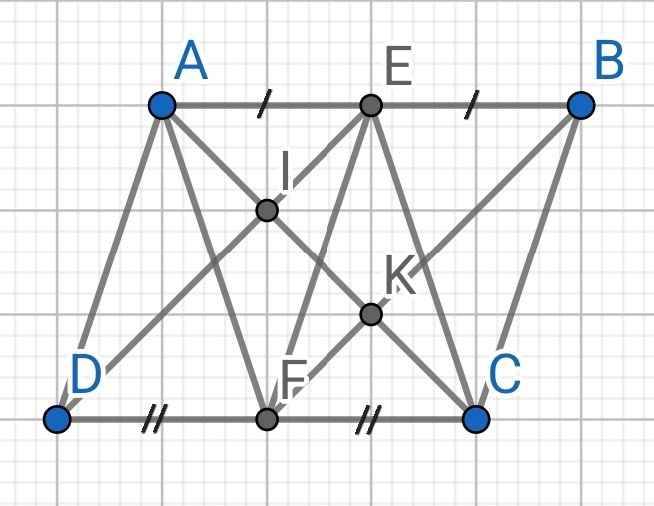 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC

A B C N M G E F I
a, xét tứ giác BICG có :
M là trung điểm cuả BC do AM là trung tuyến (gt)
M là trung điểm của GI do I đx G qua M (gt)
=> BICG là hình bình hành (dh)
+ G là trọng tâm của tam giác ABC (gt)
=> GM = AG/2 và GN = BG/2 (đl)
E; F lần lượt là trung điểm của GB; GA (gt) => FG = AG/2 và GE = BG/2 (tc)
=> FG = GM và GN = GE
=> G là trung điểm của FM và EN
=> MNFE là hình bình hành (dh)
b, MNFE là hình bình hành (câu a)
để MNFE là hình chữ nhật
<=> NE = FM
có : NE = 2/3BN và FM = 2/3AM
<=> AM = BN mà AM và BN là trung tuyến của tam giác ABC (Gt)
<=> tam giác ABC cân tại C (đl)
c, khi BICG là hình thoi
=> BG = CG
BG và AG là trung tuyến => CG là trung tuyến
=> tam giác ABC cân tại A
ABCD là hình bình hành \(\Rightarrow\) AB = CD; góc A = góc C; AD = BC
E là trung điểm của AD \(\Rightarrow\) AE = \(\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow\) FC = \(\frac{BC}{2}\)
mà AD = BC (cmt)
nên AE = FC
Xét \(\Delta\) ABE và \(\Delta\) CDF có
góc A = góc C (cmt)
AE = FC (cmt)
AB = CD (cmt)
\(\Rightarrow\) tam giác ABE = tam giác CDF (c.g.c)
\(\Rightarrow\) BE = DF