Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vi tam giac AMB can tai A nen AM=AB ma AB=DC ( ABCD la hbh ) suy ra AM=AB=CD
tuong tu BC=CN=AD
Ta co DM=AD+AM
DN=DC+CN
Ma AD=CN va AM=CD nen DM=DN suy ra tam giac DMN can tai D (dpcm)

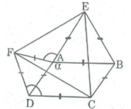
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.

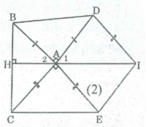
∠ (BAD) + ∠ (BAC) + ∠ (DAE) + ∠ (EAC) = 360 0
Lại có: ∠ (BAD) = 90 0 , ∠ (EAC) = 90 0
Suy ra: ∠ (BAC) + ∠ (DAE) = 180 0 (1)
AE // DI (gt)
⇒ ∠ (ADI) + ∠ (DAE) = 180 0 (2 góc trong cùng phía)
Từ (1) và (2) suy ra: ∠ (BAC) = ∠ (ADI)
Xét ∆ ABC và ∆ DAI có:
AB = AD ( vì tam giác ABD vuông cân).
AC = DI ( = AE)
∠ (BAC) = ∠ (ADI) ( chứng minh trên)
Suy ra: ∆ ABC = ∆ DAI (c.g.c) ⇒ IA = BC

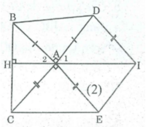
∆ ABC = ∆ DAI (chứng minh trên) ⇒ ∠ (ABC) = ∠ A 1 (3)
Gọi giao điểm IA và BC là H.
Ta có: ∠ A 1 + ∠ (BAD) + ∠ A 2 = 180 0 (kề bù)
Mà ∠ (BAD) = 90 0 (gt) ⇒ ∠ A 1 + ∠ A 2 = 90 0 (4)
Từ (3) và (4) suy ra: ∠ (ABC)+ ∠ A 2 = 90 0
Trong ∆ AHB ta có: ∠ (AHB) + ∠ (ABC)+ ∠ A 2 = 180 0
Suy ra ∠ (AHB) = 90 0 ⇒ AH ⊥ BC hay IA ⊥ BC