Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tg MOB và tg NOD có
AB//CD => ^MBO=^NDO (góc so le trong)
^MOB=^NOD (góc đối đỉnh)
OB=OD (t/c đường chéo hình bình hành)
=> tg MOB=tg NOD (g.c.g)
=> OM=ON
b/ Từ câu a có tg MOB = tg NOD => MB=ND (1)
AM=AB-MB; CN=CD-ND (2)
Do ABCD là hình bình hành => AB=CD (3)
Từ (1) (2) (3) => AM=CN mà AM//CN => AMCN là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

A B C D M N O
1) Xét tam giác AOM và tam giác CON có:
OA = OC ( O là giao điểm hai đường chéo của hình bình hành)
^AOM =^NOC ( đối đỉnh)
^MAO =NCO ( so le trong , AM// NC)
=> Tam giác AOM = tam giác CON (1)
=> OM=ON
2) Vì AB//DC
=> AM//NC
và từ (1) suy ra AM=NC
=> AMNC là hình bình hành

a) hình bình hành ABCD có:
O là giao điểm của AC và BD
=> O là trung điểm của AC và BD
xét tam giác AOM và tam giác NOC có:
AO= CO
góc A² = góc C¹ (so le trong)
góc O¹=góc O² (đối đỉnh)
=> tam giác AOM=tam giác CON(g.c.g) => OM =ON
=> M đối xứng với N qua O
b) tam giác AOM= tam giác CON nên
=> AM= CN, AM // CN
=> tứ giác AMNC là hình bình hành 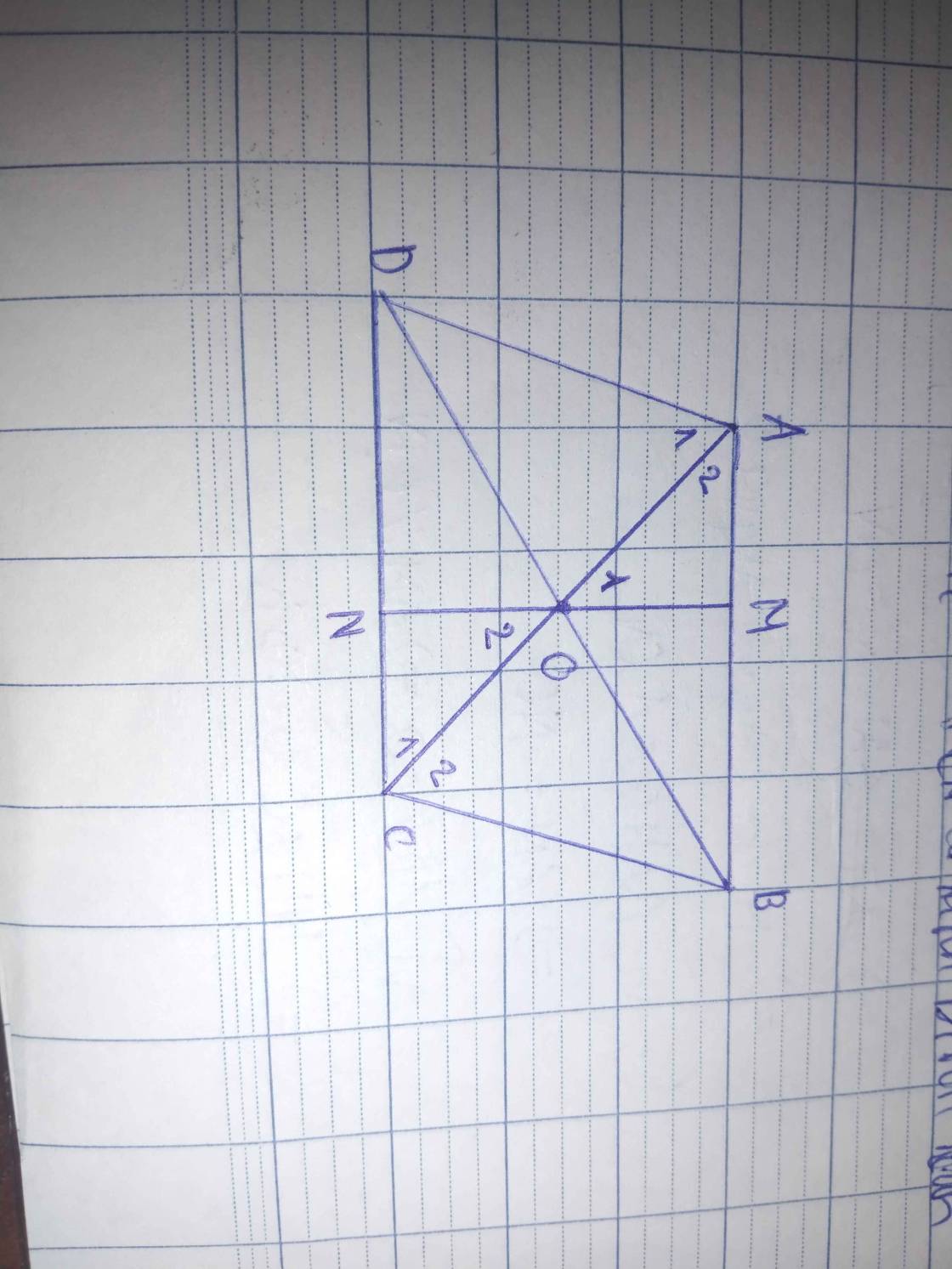
a vi o la giao diem 2 duong cheo od =ob
xet tam giac bom va tam giac don co ob bang od
obm bang odn so le trong don bang bom doi dinh
suy ra om bằng on
bvi mn va ac la 2 duong cheo ma o la trung diem mn va ac
am song song cn suy ra amcn la hinh binh hanh