
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét /\\(\) AMI:MA<MI+IA
Cộng MB vào hai vế :
MA+MB<MI+IA+MB
=>MA+MB<IB+IA (1)
Xét /\ BIC:IB<IC+CB
Cộng IA vào hai vế:
IB+IA<IC+CB+IA
=>IB+IA<CA+CB (2)
Từ (1),(2) ta có MA+MB<IA+IB<CA + CB


B = 1.2.3 + 2.3.4 + ... + (n-1)n(n+1)
=> 4B = 1.2.3.4 + 2.3.4.4 + ... + (n-1)n(n+1)4
= 1.2.3.(4-0) + 2.3.4.(5-1) + ... + ((n-1)n(n+1)[(n+2) - (n-2)
= 1.2.3.4 + 2.3.4.5 - 1.2.3.4 + ... + (n-1)n(n+1)(n+2) - (n-2)(n-1)n(n+1)
= (n-1)n(n+1)(n+2)
=> B = \(\frac{\left(n-1\right)n\left(n+1\right)\left(n+2\right)}{4}\)

Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)

a)Ta có:\(\Delta\)NMP cân tại N
=> ^NMP = ^NPM = 1800 − ^NMP = 1800 − ^NPM
=> ^NMA = ^NPB
Xét \(\Delta\)NMA và \(\Delta\) NPB có:
\(\hept{\begin{cases}NM=NP\left(gt\right)\\\widehat{NMA}=\widehat{NPB}\left(cmt\right)\\MA=PB\left(gt\right)\end{cases}\Rightarrow\Delta NMA=\Delta NPB\left(c.g.c\right)}\)
=> NA = NB (2 cạnh tương ứng)
=> \(\Delta\)NAB cân tại N
b)Từ \(\Delta\)NMA = \(\Delta\)NPB (cmt )
=> ^NAM = ^NBP (2 góc tương ứng) hay ^HAM = ^KBP
Xét \(\Delta\)HAM vuông tại H và \(\Delta\)KBP vuông tại K có:
\(\hept{\begin{cases}AM=BP\left(gt\right)\\\widehat{HAM}=\widehat{KBP}\left(cmt\right)\\\Delta HAM=\Delta KBP\left(ch-gn\right)\end{cases}}\)
=> HM = KP (2 cạnh tương ứng)

BT33a.
Đặt \(A=0,5\left(2007^{2005}-2003^{2003}\right)=\dfrac{2007^{2005}-2003^{2003}}{2}\)
Để \(A\in Z\Leftrightarrow A⋮2\Leftrightarrow2007^{2005}-2003^{2003}⋮2\)
Ta có: \(7^1=7\\ 7^2=\overline{...9}\\ 7^3=\overline{...3}\\ 7^4=\overline{...1}\\ 7^5=\overline{...7}\) . Vậy chu kì lũy thừa cơ số 7 là 4
\Và: \(3^1=3\\ 3^2=9\\ 3^3=\overline{...7}\\ 3^4=\overline{...1}\\ 3^5=\overline{...3}\). Vậy chu kì lũy thừa cơ số 3 là 4
Ta có: \(2005\div4=501\)(dư 1)\(\Rightarrow2007^{2005}=\overline{...7}\)
Và: \(2003\div4=500\)(dư 3)\(\Rightarrow2003^{2003}=\overline{...7}\)
Vậy \(2007^{2005}-2003^{2003}=\overline{...7}-\overline{...7}=\overline{...0}⋮2\)
Vậy \(A\in Z\left(đpcm\right)\)


1)\(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}\)
\(A< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}-\dfrac{1}{100}\)
\(A< \dfrac{1}{4}\)(1)
\(A>\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{100.101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(A>\dfrac{1}{5}-\dfrac{1}{101}\)
\(A>\dfrac{96}{505}>\dfrac{1}{6}\)
\(A>\dfrac{1}{6}\)(2)
Từ (1) và (2)
\(\dfrac{1}{6}< A< \dfrac{1}{4}\)
2)
\(A=\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{92.95}+\dfrac{1}{95.98}\)
\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{92}-\dfrac{1}{95}+\dfrac{1}{95}-\dfrac{1}{98}\right)\)\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{98}\right)\)
\(A=\dfrac{1}{3}.\dfrac{24}{49}=\dfrac{8}{49}\)



 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 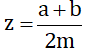 thì ta có x < z < y.
thì ta có x < z < y.


Cho hình bên ??? Where's hình?
A A A B B B C C C I I I M M M
Trong \(\Delta AMI\),ta có :
MA < IA + IM <=> MA + MB < IA + IM + MB
<=> MA + MB < IA + IB(1)
Trong \(\Delta BCI\),ta có : IB < CI + CB <=> IA + IB < IA + CI + CB
<=> IA + IB < CA + CB (2)
Từ (1) và (2) => MA + MB < IA + IB < CA + CB