Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(V_1=\pi\int\limits^9_0xdx=\frac{81\pi}{2}\)
Gọi \(M\left(a;\sqrt{a}\right)\) (\(0\le a\le9\)) và \(N\left(a;0\right)\) là hình chiếu của M trên Ox
Khi quay AOM quanh Ox sẽ tạo thành hai hình nón chung đáy với bán kính đáy \(r=MN=y_M=\sqrt{a}\); chiều cao lần lượt là \(ON=x_N=a\) và \(OM=x_M-x_N=9-a\)
\(\Rightarrow V_2=\frac{1}{3}\pi\left(\sqrt{a}\right)^2\left(a+9-a\right)=3\pi a\)
\(\Rightarrow\frac{81\pi}{2}=6\pi a\Rightarrow a=\frac{27}{4}\) \(\Rightarrow M\left(\frac{27}{4};\frac{3\sqrt{3}}{2}\right)\)
\(\Rightarrow\) diện tích phần giới hạn:
\(S=\int\limits^{\frac{27}{4}}_0\sqrt{x}dx-\frac{1}{2}.\frac{27}{4}.\frac{3\sqrt{3}}{2}=\frac{27\sqrt{3}}{4}-\frac{81\sqrt{3}}{16}=\frac{27\sqrt{3}}{16}\)

4.
Gọi M là trung điểm CD, qua M kẻ đường thẳng song song AB
Gọi N là trung điểm AB, qua N kẻ đường thẳng song song AM
Gọi giao của 2 đường thẳng trên là O \(\Rightarrow\) O là tâm (S)
\(\Rightarrow AO=R=\sqrt{3}\)
Đặt \(AB=x;AC=y;AD=z\)
\(AN=\frac{AB}{2}=\frac{x}{2}\) ; \(AM=\frac{CD}{2}=\frac{1}{2}\sqrt{AC^2+AD^2}=\frac{1}{2}\sqrt{y^2+z^2}\)
Áp dụng Pitago: \(AO^2=AN^2+AM^2\)
\(\Rightarrow\frac{x^2}{4}+\frac{1}{4}\left(y^2+z^2\right)=3\Rightarrow x^2+y^2+z^2=12\)
\(V=\frac{1}{3}xyz\le\frac{1}{3}\left(\frac{x+y+z}{3}\right)^3\le\frac{1}{3}\left(\frac{\sqrt{3\left(x^2+y^2+z^2\right)}}{3}\right)^3=\frac{8}{3}\)
2.
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a}{2}\)
Áp dụng công thức từ câu 1:
\(R=\frac{SA^2}{2SO}=\frac{3a}{4}\)
3.
\(BC=AB\sqrt{2}=2a\)
Gọi H là hình chiếu của S lên (ABC) \(\Rightarrow\) H đồng thời là tâm đường tròn ngoại tiếp đáy
\(\Rightarrow\) H là trung điểm BC
\(\Rightarrow\widehat{SAH}=60^0\Rightarrow SH=AH.tan60^0=\frac{BC}{2}tan60^0=a\sqrt{3}\)
\(SA=\frac{AH}{cos60^0}=2a\)
\(\Rightarrow R=\frac{SA^2}{2SH}=\frac{2\sqrt{3}a}{3}\)
\(S=4\pi R^2=\frac{16\pi a^2}{3}\)

Câu 5:
Tương tự câu 4, ta thấy tâm $I$ của khối cầu ngoại tiếp $S.ABCD$ là trung điểm $SC$
Theo định lý Pitago:
$SA^2=SB^2-AB^2=(a\sqrt{3})^2-a^2=2a^2$
$AC^2=AB^2+BC^2=a^2+a^2=2a^2$
$SC=\sqrt{SA^2+AC^2}=\sqrt{2a^2+2a^2}=2a$
Do đó: $R=SI=IC=\frac{SC}{2}=a$
Thể tích khối cầu ngoại tiếp S.ABCD là:
$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi a^3$
Đáp án A
Câu 4:
$AC=\sqrt{AB^2+AD^2}=2a$
$(SC, (ABCD))=\widehat{SCA}=60^0$
$\Rightarrow \frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{3}.AC=2\sqrt{3}a$
$SC=\sqrt{SA^2+AC^2}=\sqrt{(2\sqrt{3}a)^2+(2a)^2}=4a$
Gọi $I$ tâm mặt cầu ngoại tiếp hình chóp. $IS=IA=IC$ nên $I$ là tâm ngoại tiếp tam giác $SAC$
$\Rightarrow I$ là trung điểm $SC$.
Bán kính $IS=IC=\frac{AC}{2}=\frac{4a}{2}=2a$
Đáp án A

Câu 1:
\(\overrightarrow{MN}=\left(3;-1;-4\right)\Rightarrow\) pt mặt phẳng trung trực của MN:
\(3\left(x-\frac{7}{2}\right)-\left(y-\frac{1}{2}\right)-4\left(z-2\right)=0\Leftrightarrow3x-y-4z-2=0\)
\(\overrightarrow{PN}=\left(4;3;-1\right)\Rightarrow\) pt mp trung trực PN: \(4x+3y-z-7=0\)
\(\Rightarrow\) Phương trình đường thẳng giao tuyến của 2 mp trên: \(\left\{{}\begin{matrix}x=1+t\\y=1-t\\z=t\end{matrix}\right.\)
\(\Rightarrow I\left(1+c;1-c;c\right)\) \(\Rightarrow\overrightarrow{NI}=\left(c-4;1-c;c\right)\)
\(d\left(I;\left(Oyz\right)\right)=IN\Rightarrow\left|1+c\right|=\sqrt{\left(c-4\right)^2+\left(1-c\right)^2+c^2}\)
\(\Leftrightarrow\left(c+1\right)^2=3c^2-10c+17\)
\(\Leftrightarrow2c^2-12c+16=0\Rightarrow\left[{}\begin{matrix}c=4\\c=2\end{matrix}\right.\)
Mà \(a+b+c< 5\Rightarrow\left(1+c\right)+\left(1-c\right)+c< 5\Rightarrow c< 3\Rightarrow c=2\)
Câu 2:
Phương trình tham số d: \(\left\{{}\begin{matrix}x=-1+2t\\y=t\\z=2-t\end{matrix}\right.\) \(\Rightarrow C\left(-1+2n;n;2-n\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2n;n-3;1-n\right)\\\overrightarrow{AB}=\left(1;-1;-2\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(3n-7;-3n-1;3n-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(3n-7\right)^2+\left(-3n-1\right)^2+\left(3n-3\right)^2}=4\sqrt{2}\)
\(\Leftrightarrow27n^2-54n+27=0\Rightarrow n=1\)
\(\Rightarrow C\left(1;1;1\right)\Rightarrow m+n+p=3\)

11.
Thay tọa độ M vào pt d ta được:
\(\frac{1}{1}=\frac{3}{3}=\frac{m}{-2}\Rightarrow m=-2.1=-2\)
12.
\(AA'\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của A'B lên (ABC)
\(\Rightarrow\widehat{A'BA}\) là góc giữa A'B và (ABC)
\(\Rightarrow\widehat{A'BA}=60^0\)
\(AB=\frac{AC}{\sqrt{2}}=2a\Rightarrow AA'=AB.tan60^0=2a\sqrt{3}\)
8.
\(I=2\int\limits^9_0f\left(x\right)dx+3\int\limits^9_0g\left(x\right)dx=2.37+3.???=...\)
Đề thiếu, bạn tự điền số và tính
9.
\(z=\frac{1}{3-4i}=\frac{3+4i}{\left(3-4i\right)\left(3+4i\right)}=\frac{3}{25}+\frac{4}{25}i\)
\(\Rightarrow\overline{z}=\frac{3}{25}-\frac{4}{25}i\)
10.
\(\overline{z_1}=1-5i\) \(\Rightarrow\overline{z_1}+iz_2=1-5i+i\left(3-2i\right)=3-2i\)
Điểm biểu diễn là \(Q\left(3;-2\right)\)
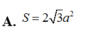
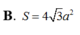
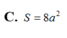
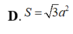

Đáp án A