Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)

giải
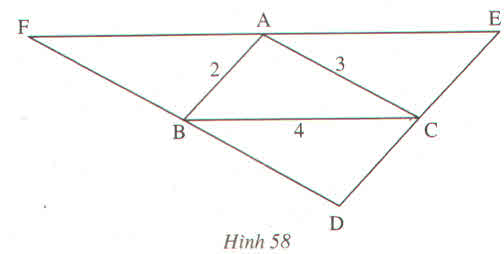
*xét tam giác abc và tam giác abf có
góc abc=góc bà(so le trong)
ad;chung
góc bac=góc abf(so le trong)
suy ra tam giác abc=tam giác abf(gcg)
suy ra af=bc=4(2 cạnh tương ứng)
bf=ac=3
*xét tam giác abc và tam giác ace có
góc acb=góc cae(số lẻ trong)
ac; chung
gốc bac= gốc eca(slt)
suy ra tam giác abc= tam giác ace
suy ra ae=bc=4(2 cạnh tương ứng)
ce=ab=2
* xét tam giác abc và tam giác dcb có
góc acb= góc dbc(slt)
bc;chung
góc abc= góc dcb
suy ra tam giác abc=tam giác dcb
suy ra dc=ab=2
db=ac=3
ta có ef=ae+af=4+4=8
df=db+bf=3+3=6
de=dc+ce=2+2=4
vậy chu vi của tam giác def là
để+DF+EF=4+6+8=18(ĐƠN VỊ ĐO ĐỘ DÀI)

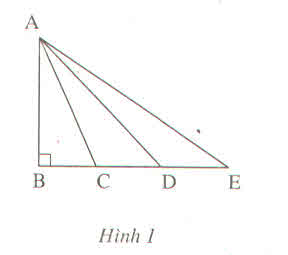
Điểm C nằm giữa B và D nên BC < BD (1)
Điểm C nằm giữa B và E nên BD < BE (2)
Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra
BC < BD < BE
AB⊥BE
Suy ra: AB < AC < AD < AE.


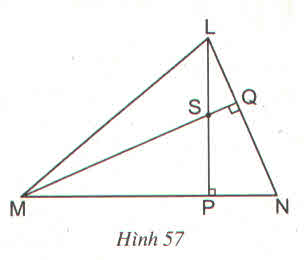
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)

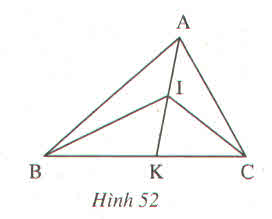
a)Ta có \(\widehat{BIK}\) là góc ngoài của BAI.
Nên \(\widehat{BIK}>\widehat{BAI}\) (1)
b) \(\widehat{CIK}>\widehat{CAI}\)( Góc ngoài của \(\Delta\) CAI)
Từ (1) và (2) ta có:
\(\widehat{BIK}+\widehat{CIK}>\widehat{BAI}+\widehat{CAI}\)
\(\Rightarrow\widehat{BIC}>\widehat{BAC}\)
) Ta có ∠BIK là góc ngoài của ∠BAI( hay là góc ngoài ∠BAK)
Các em lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên ∠BIK > ∠BAK (1)
b) Góc ∠CIK > ∠CAI (2) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: ∠BIK + ∠CIK > ∠BAK + ∠CAI
Mà ∠BIC = ∠BIK + ∠CIK; ∠BAC = ∠BAK + ∠CAI
⇒ ∠BIC > ∠BAC.

B A C M K H G I
a) Xét hai tam giác MHB và MKC có:
MB = MC (gt)
Góc HMB = góc KMC (đối đỉnh)
MH = MK (gt)
Vậy: tam giác MHB = tam giác MKC (c - g - c)
c) Ta có: AM = MB = MC = \(\dfrac{1}{2}\) BC (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
=> Tam giác MAB cân tại M
=> MH là đường cao đồng thời là đường trung tuyến
hay HB = HA
=> CH là đường trung tuyến ứng với cạnh AB
Hai đường trung tuyến AM và CH cắt nhau tại G
=> G là trọng tâm của tam giác ABC
Mà BI đi qua trọng tâm G (G thuộc BI)
Do đó BI là đường trung tuyến còn lại
hay I là trung điểm của AC (đpcm).

Ta có tam giác ABC vuông ở A nên
\(\widehat{ABC}+\widehat{C}_1=90^0\)
Trong đó tam giác OCD vuông ở D có \(\widehat{MOP}=\widehat{C}_2=90^0\)
Nên \(\widehat{MOP}=\widehat{ABC}\)
\(\widehat{MOP}=32^0\)
Ta có tam giác ABC vuông ở A nên ∠ABC + ∠BCA = 900
Trong đó tam giác OCD vuông ở D có ∠COD + ∠OCD = 900
mà góc ∠BCA = ∠OCD ( 2 góc đối đỉnh)
Từ (1),(2),(3) ∠COD = ∠ABC mà ∠ABC= 320 . Nên ∠COD = 320
hay chính là ∠MOP =320
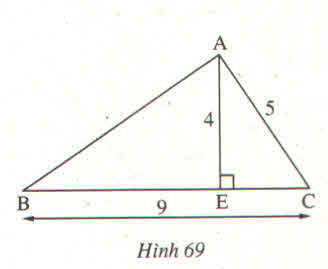





Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)