K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 4 2017
Hướng dẫn:
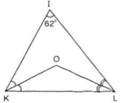
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210
c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
11 tháng 5 2019
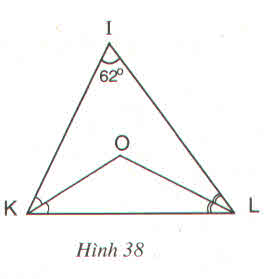
a, Áp dụng định lí tổng 3 góc trong ΔIKL, ta có:
∠I + ∠IKL + ∠ILK= 180 độ
⇒ ∠IKL + ∠ILK= 180 độ - ∠I
OK, OL là phân giác của các góc K, L nên:
∠OKL= 1/2∠IKL, ∠OLK= 1/2∠ILK
⇒ ∠OKL + ∠OLK= 1/2 (∠IKL + ∠ILK)
= 1/2 . (180 độ - ∠I)
Áp dụng định lí tổng 3 góc trong ΔOKL có:
∠ KOL + ∠OKL + ∠OLK = 180 độ
⇒ ∠KOL= 180 độ - (∠OKL + ∠OLK)
= 180 độ - 180- ∠I / 2= 180 + ∠I/2
Mà ∠I= 62 độ nên:
∠KOL= 180 +62/2= 121 độ
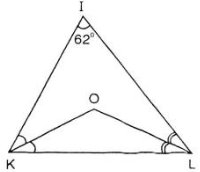
b, Ta có: 3 đường phân giác trong tam giác đồng quy.
Mà 2 đường phân giác KO, LO cắt nhau tại O
⇒ OI là tia phân giác của ∠KIL
⇒ ∠KIO= 1/2 ∠KIL= 1/2. 62 độ= 31 độ
c, O là giao điểm 3 đường phân giác của ΔIKL. Áp dụng định lí 3 đường phân giác
Vậy O cách đều 3 cạnh của ΔIKL
U
11 tháng 3 2018
b) ΔKIL có O là giao điểm của hai đường phân giác KO và LO nên OI là đường phân giác của góc KIL (định lí ba đường phân giác cùng đi qua một điểm).
Do đó:
c) Điểm O có cách đều 3 cạnh của tam giác IKL bởi vì O là giao điểm của ba đường phân giác trong tam giác đó.
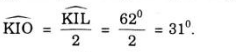
Ta có : ba đường phân giác trong tam giác đồng quy.
Mà hai đường phân giác KO, LO cắt nhau tại O