QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
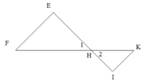
a) Vì \(\widehat {MNE} = \widehat {NEF}( = 30^\circ )\), mà 2 góc này ở vị trí so le trong nên MN//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì \(\widehat {DKH} = \widehat {DFE}( = 60^\circ )\), mà 2 góc này ở vị trí đồng vị nên HK//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)
c) Vì MN//EF; HK//EF nên HK//MN
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
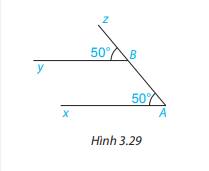
Vì \(\widehat {xAz} = \widehat {yBz}( = 50^\circ )\)
Mà hai góc này ở vị trí đồng vị nên Ax//By (Dấu hiệu nhận biết hai đường thẳng song song)
CM
24 tháng 3 2017
Cho hình vẽ, biết :
a) T a có: A ^ 1 = A ^ 2 = 70 0 (đối đỉnh).
Do đó A ^ 1 + B ^ = 70 0 + 110 0 = 180 0
Suy ra Ax//By (vì có cặp góc trong cùng phía bù nhau).
b) Ta có: F ^ = H ^ 1 ; K ^ = H ^ 2 mµ H ^ 1 = H ^ 2 ( đối đỉnh)
nên F ^ = K ^ . Suy ra EF//IK( vì có cặp góc so le trong bằng nhau).
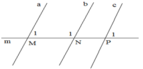
Ta có : M ^ 1 = P ^ 1 = 75 0 .
Suy ra a//c( vì có cặp góc đồng vị bằng nhau)
Ta có:
b N P ^ kÒ bï víi gãc N 1 , d o ®ã: b N P ^ = 180 0 − 105 0 = 75 0 VËy b N P ^ = P 1 ^ = 70 0
Suy ra b//c (vì có cặp góc đồng vị bằng nhau)
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
PT
1
CM
15 tháng 6 2018
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
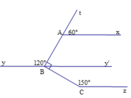
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
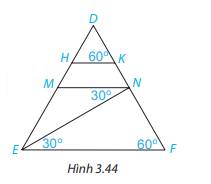
a) Vì \(\widehat {xAB} = \widehat {ABy}( = 45^\circ )\)
Mà hai góc này ở vị trí so le trong
Do đó, xx’ // By ( Dấu hiệu nhận biết 2 đường thẳng song song) hay Ax’ // By
b)
Cách 1:
Vì Ax’ // By nên \(\widehat{x'HK}=\widehat{HKB}\) (2 góc so le trong)
Mà \(\widehat{x'HK}=90^0\) nên \(\widehat{HKB}=90^0\)
Do đó, Ax’ \( \bot \) HK
Cách 2:
Vì Ax’ // By, mà By \( \bot \) HK nên Ax’ \( \bot \) HK (đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia)