Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:
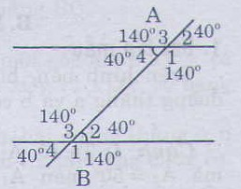
c) Ta có:
góc A4 + A1 = 180độ
=> góc A1 = 180 độ - 40 độ = 140 độ
=> góc A1 + góc B2= 40độ + 140 độ = 180 độ
Ý 2
Ta có:
góc B3 + góc B2 = 180 độ
=> góc B3 = 180 độ - 40 độ = 140 độ
=> góc A4 + B3 = 140 độ + 40 độ = 180 độ

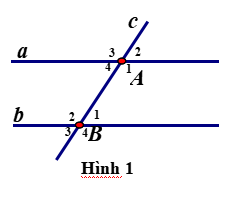
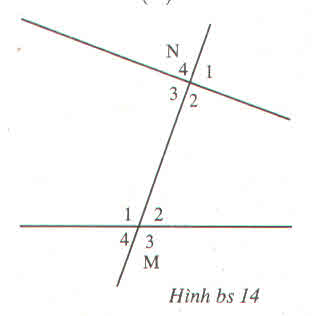
a) ˆB3B3^
b) ˆB2B2^
c) 1800 ; là cặp góc trong cùng phía
d) Bằng cặp góc so le trong ˆB2B2^=ˆA4A4^.
a) \(\widehat{A_1}\)\(=\widehat{B_3}\)(vì là cặp góc so le trong)
b)\(\widehat{A_2}\)\(=\widehat{B_2}\)(vì là cặp góc đồng vị)
c)\(\widehat{B_3}\)\(+\widehat{A_4}\)\(=180^0\)(vì là cặp góc trong cùng phía)
d)\(\widehat{A_2}\)\(=\widehat{B_4}\)(vì là cặp góc cùng bằng \(\widehat{A_4}\) )
Ủng hộ mk nhé!!! ^.^

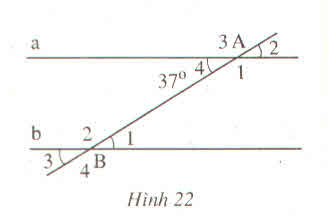
Vì a // b nên ta có:
a) ^B1 = ^A4 = 37° (2 góc so le trong)
Vậy ^B1 = 37°.
b) ^A1 = ^B4 (2 góc đồng vị).
c) ^B2 + ^A4 = 180° (2 góc trong cùng phía)
hay ^B2 + 37° =180°.
=> ^B2 = 180° - 37° = 143°.
Vậy ^B2 = 143°.

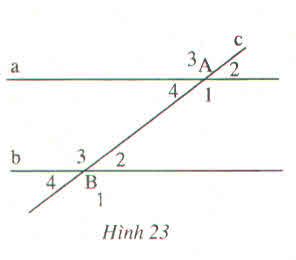
a: dong vi
b: trong cung phia
c :đổng vị
d :ngoài cùng phía
e :???
g:CDE,MED
h:DBC,EBA
a)...đồng vị
b)...trong cùng phía
c)...đồng vị
d)...ngoài cùng phía
e)...so le trong
g)...MED và EDC
h)...MED và EBC
tớ thấy cậu ghi sai đề rồi tớ chỉ làm theo sách

Bài 20 (Sách bài tập - tập 1 - trang 105)
Trên hình 5 người ta cho biết a // b và P1ˆ=Qˆ1=300P1^=Q^1=300

a) Viết tên một cặp góc đồng vị khác và nói rõ số đo mỗi góc
b) Viết tên một cặp góc so le trong và nói rõ số đo của mỗi góc
c) Viết tên một cặp góc trong cùng phía và nói rõ số đo mỗi góc
d) Viết tên một cặp góc ngoài cùng phía và cho biết tổng số đo hai góc đó







\(a,\text{So le trong: }\widehat{A_1}\text{ và }\widehat{B_2}\\ \text{Đồng vị: }\widehat{A_1}\text{ và }\widehat{B_4}\\ b,a\text{//}b\Rightarrow\widehat{A_1}=\widehat{B_2}=42^0\\ \Rightarrow\widehat{B_1}=180^0-\widehat{B_2}=138^0\left(\text{kề bù}\right)\)
giúp mik tìm thêm so le trong và đồng vị thêm một cặp góc nx ik bạn