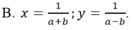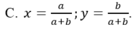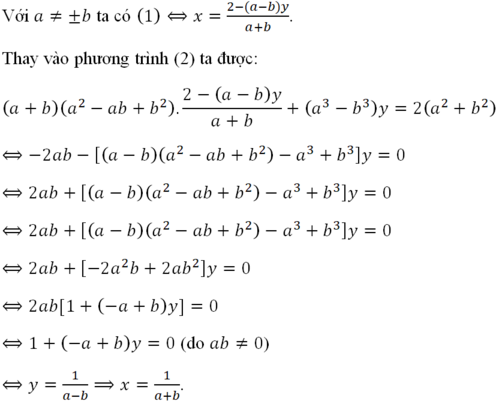Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có D = m − 1 2 m = m 2 + 2 > 0 , ∀ m ∈ R nên hệ phương trình luôn có nghiệm duy nhất
D x = 3 − 1 9 m = 3 m + 9 ; D y = m 3 2 9 = 9 m − 6
Vậy hệ luôn có nghiệm duy nhất là: x = 3 m + 9 m 2 + 2 y = 9 m − 6 m 2 + 2
Ta có: A = 3 x − y = 3 3 m + 9 m 2 + 2 − 9 m − 6 m 2 + 2 = 33 m 2 + 2
Vì m ∈ Z nên để A nguyên thì m 2 + 2 là ước của 33 mà m 2 + 2 ≥ 2 nên ta có các trường hợp sau:

Mà m nguyên dương nên m ∈ 1 ; 3
Vậy có 2 giá trị nguyên dương của m để A nguyên.
Đáp án cần chọn là: B

Bài 1:
Khi $m=1$ thì HPT trở thành:
\(\left\{\begin{matrix} x-2y=-1\\ 2x+y=2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x-4y=-2\\ 2x+y=2\end{matrix}\right.\)
\(\Rightarrow (2x+y)-(2x-4y)=2-(-2)\)
\(\Leftrightarrow 5y=4\Rightarrow y=\frac{4}{5}\)
\(x=\frac{2-y}{2}=\frac{2-\frac{4}{5}}{2}=\frac{3}{5}\)
Vậy ...........
b)
HPT \(\Leftrightarrow \left\{\begin{matrix} mx-2y=m-2\\ y=m+1-2x\end{matrix}\right.\Rightarrow mx-2(m+1-2x)=m-2\)
\(\Leftrightarrow x(m+4)=3m(*)\)
Để HPT ban đầu có bộ nghiệm (x,y) duy nhất thì PT $(*)$ phải có nghiệm $x$ duy nhất. Điều này xảy ra khi $m+4\neq 0$ hay $m\neq -4$
Bài 2:
a)
Khi $m=2$ thì hệ trở thành:
\(\left\{\begin{matrix}
x+2y=1\\
2x+y=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
2x+4y=2\\
2x+y=1\end{matrix}\right.\)
\(\Rightarrow (2x+4y)-(2x+y)=2-1\)
\(\Leftrightarrow 3y=1\Rightarrow y=\frac{1}{3}\)
Khi đó: \(x=1-2y=1-2.\frac{1}{3}=\frac{1}{3}\)
Vậy HPT có bộ nghiệm duy nhất $(x,y)=(\frac{1}{3}, \frac{1}{3})$
b)
HPT \(\Leftrightarrow \left\{\begin{matrix} x=1-my\\ mx+y=1\end{matrix}\right.\Rightarrow m(1-my)+y=1\)
\(\Leftrightarrow y(1-m^2)=1-m(*)\)
Để HPT ban đầu có nghiệm duy nhất thì PT $(*)$ cũng phải có nghiệm duy nhất. Điều này xảy ra khi \(1-m^2\neq 0\Leftrightarrow m\neq \pm 1\)
Khi đó:
\(y=\frac{1-m}{1-m^2}=\frac{1}{1+m}\)
\(x=1-my=1-\frac{m}{m+1}=\frac{1}{m+1}\)
Vậy HPT có nghiệm \((x,y)=(\frac{1}{m+1}, \frac{1}{m+1})\)
Để \(x,y>0\Leftrightarrow \frac{1}{m+1}>0\Leftrightarrow m>-1\)
Kết hợp những điều vừa tìm được suy ra $m>-1$ và $m\neq 1$ thì thỏa mãn.

a) Khi m=1 hpt có vô số nghiệm
Khi m=-1 hpt vô nghiệm
Khi \(m\ne\pm1\Rightarrow\left\{{}\begin{matrix}y=2m-mx\\x+m\left(2m-mx\right)=m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2m-mx\\x=\dfrac{2m^2-m-1}{\left(m^2-1\right)}=\dfrac{2m+1}{m+1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+1}{m+1}\\y=\dfrac{m}{m+1}\end{matrix}\right.\)
b)\(\left\{{}\begin{matrix}x=\dfrac{2m+1}{m+1}\left(1\right)\\y=\dfrac{m}{m+1}\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow x\left(m+1\right)=2m+1\Leftrightarrow mx+x=2m+1\Leftrightarrow m=\dfrac{1-x}{x-2}\left(3\right)\)
Thay \(\left(3\right)\) vào \(\left(2\right):y=\dfrac{\dfrac{1-x}{x-2}}{\dfrac{1-x}{x-2}+1}=x-1\)

Hệ pt : \(\begin{cases}x+my=m+1\\mx+y=3m-1\end{cases}\)
Xét pt đầu : \(x+my=m+1\Leftrightarrow x=m+1-my\) thay vào pt còn lại :
\(m\left(m+1-my\right)+y=3m-1\)
\(\Leftrightarrow y\left(1-m^2\right)=-m^2+2m-1\)
Nếu \(m=1\) thì pt có dạng 0.y = 0 => Vô số nghiệm.
Nếu m = -1 thì pt có dạng 0.x = -4 => vô nghiệm.
Xét với \(m\ne1\) và \(m\ne-1\) thì pt có nghiệm \(y=\frac{-\left(m-1\right)^2}{\left(1-m\right)\left(1+m\right)}=\frac{m-1}{m+1}\)
\(\Rightarrow x=m+1-m\left(\frac{m-1}{m+1}\right)=m+1-\frac{m^2-m}{m+1}=\frac{m^2+2m+1-m^2+m}{m+1}=\frac{3m+1}{m+1}\)
Xét \(xy=\frac{\left(m-1\right)\left(3m+1\right)}{\left(m+1\right)^2}=\frac{3m^2-2m-1}{\left(m+1\right)^2}\)
Đặt \(t=m+1\) thì \(m=t-1\) thay vào biểu thức trên được
\(\frac{3\left(t-1\right)^2-2\left(t-1\right)-1}{t^2}=\frac{3t^2-8t+4}{t^2}=\frac{4}{t^2}-\frac{8}{t}+3\)
Lại đặt \(a=\frac{1}{t}\) thì : \(4a^2-8a+3=4\left(a-1\right)^2-1\ge-1\)
Suy ra \(xy\ge-1\) . Dấu đẳng thức xảy ra khi \(a=1\Leftrightarrow t=1\Leftrightarrow m=0\)
Vậy với m = 0 thì xy đạt giá trị nhỏ nhất bằng -1

Viết lại hệ \(\left\{{}\begin{matrix}2x+y=5\\-x+2y=a+5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\-2x+4y=2a+10\end{matrix}\right.\)
\(\Rightarrow5y=2a+15\Leftrightarrow y=\dfrac{2a+15}{5}\)
\(\Leftrightarrow x=2y-a-5=\dfrac{5-a}{5}\)
\(xy=\dfrac{5-a}{5}.\dfrac{2a+15}{5}=\dfrac{-2a^2-5a+75}{25}=\dfrac{-\left(a+\dfrac{5}{4}\right)^2+\dfrac{625}{8}}{25}\le\dfrac{25}{8}\)
\(max=\dfrac{25}{8}\Leftrightarrow a=-\dfrac{5}{4}\)