Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Với m=2 thì hpt trở thành:
x-2y=5
2x-y=7
<=>
2x-4y=10
2x-y=7
<=>
-3y=3
2x-y=7
<=>
y=-1
x=3
b)\(\int^{\left(m-1\right)x-my=3m-1}_{2x-y=m+5}\Leftrightarrow\int^{x=\frac{3m+my-1}{m-1}}_{\frac{6m+2my-2}{m-1}-y=m+5}\Leftrightarrow\int^{x=\frac{3m+my-1}{m-1}}_{m^2+2m+my+y+3=0}\)
*m2+2m+my+y+3=0
<=>y.(m+1)=-m2-2m-3
*Với m=-1 =>PT vô nghiệm
*Với m khác -1 =>PT có nghiệm là: \(y=\frac{-m^2-2m-3}{m+1}=-m-1-\frac{2}{m+1}\)
bí tiếp

a: Khi m=3 thì hệ phương trình sẽ là:
\(\left\{{}\begin{matrix}3x-y=2\\2x+3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x-3y=6\\2x+3y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}11x=11\\3x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3x-2=3-2=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}mx-y=2\\2x+my=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\2x+m\left(mx-2\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+2\right)=5+2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x=\dfrac{2m+5}{m^2+2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m^2+5m}{m^2+2}-2=\dfrac{2m^2+5m-2m^2-4}{m^2+2}=\dfrac{5m-4}{m^2+2}\\x=\dfrac{2m+5}{m^2+2}\end{matrix}\right.\)
\(x+y=1-\dfrac{m^2}{m^2+2}\)
=>\(\dfrac{5m-4+2m+5}{m^2+2}=\dfrac{m^2+2-m^2}{m^2+2}=\dfrac{2}{m^2+2}\)
=>7m+1=2
=>7m=1
=>\(m=\dfrac{1}{7}\)

a. Với `m=1`, ta có HPT: \(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-6\\3y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=8\end{matrix}\right.\)
b. Theo đề bài `=>` \(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\\2x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mx+2y=18\\x=1\\y=7\end{matrix}\right.\)
`=> m=4`

Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{2}\ne\dfrac{2}{-4}=-\dfrac{1}{2}\)
=>\(m\ne-1\)
\(\left\{{}\begin{matrix}mx+2y=1\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx+4y=2\\2x-4y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m+2\right)=5\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\4y=2x-3=\dfrac{10}{2m+2}-3=\dfrac{10-6m-6}{2m+2}=\dfrac{-6m+4}{2m+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\y=\dfrac{-6m+4}{8m+8}=\dfrac{-3m+2}{4m+4}\end{matrix}\right.\)
x-3y=7/2
=>\(\dfrac{5}{2m+2}-\dfrac{3\cdot\left(-3m+2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+3\left(3m-2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+9m-6}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{9m+4}{4m+4}=\dfrac{7}{2}\)
=>7(4m+4)=2(9m+4)
=>28m+28=18m+8
=>10m=-20
=>m=-2(nhận)

\(\left\{{}\begin{matrix}5x=5m\\y=2x-m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=10-m+1=11-m\end{matrix}\right.\)
Thay vào ta đc
\(2m^2-3\left(11-m\right)=2\Leftrightarrow2m^2-33+3m=2\Leftrightarrow2m^2+3m-35=0\Leftrightarrow m=\dfrac{7}{2};m=-5\)
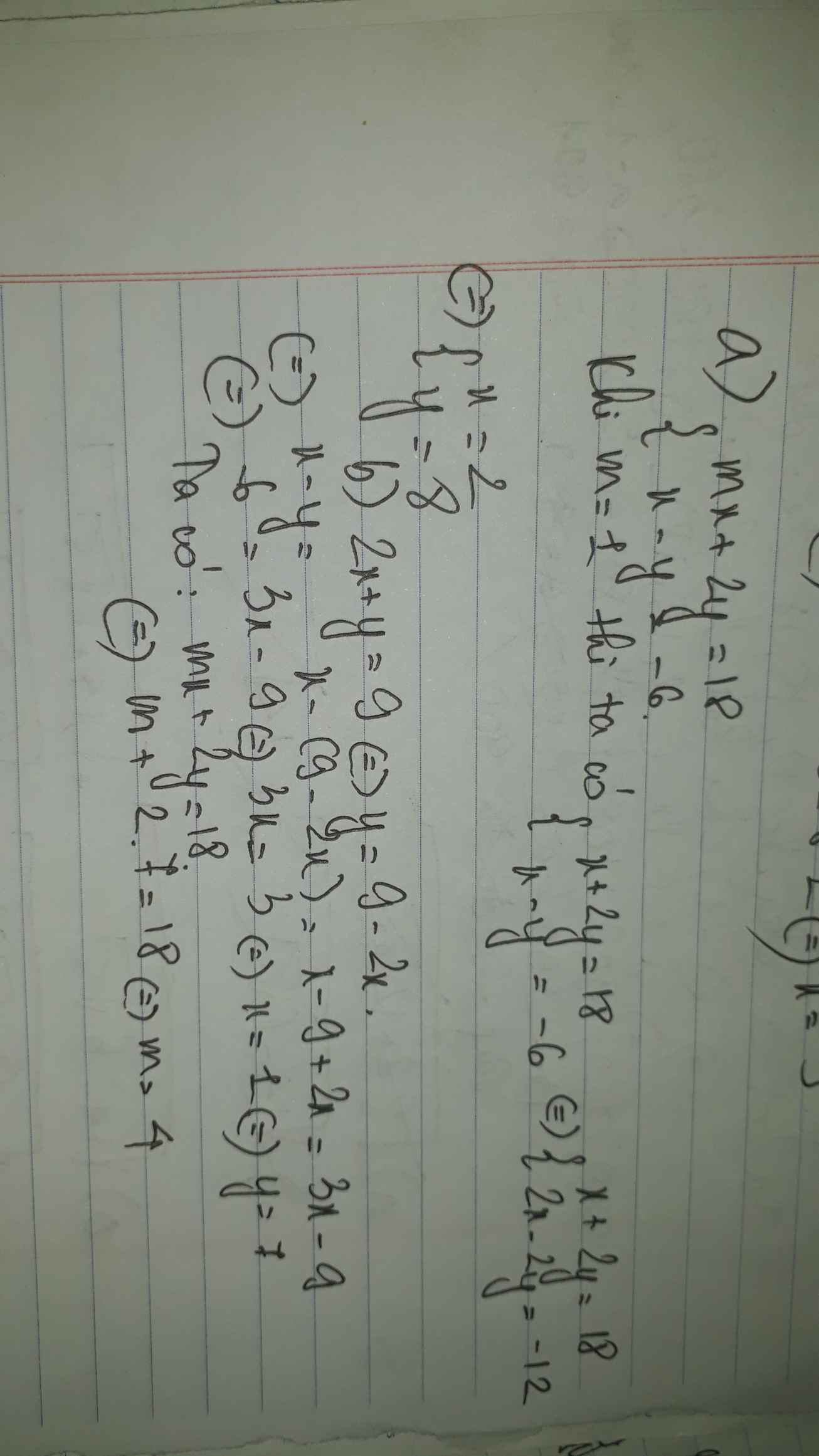
Lời giải:
a. Với $m=2$ thì:
$2x-y=1$
$2x+y=9$
Cộng 2 phép tính với nhau thì:
$2x-y+2x+y=10$
$\Rightarrow 4x=10\Rightarrow x=2,5$
$y=2x-1=2.2,5-1=4$
Vậy hpt có nghiệm $(x;y)=(2,5; 4)$
b.
$2x-y=m-1$
$2x+y=4m+1$
$\Rightarrow (2x-y)+(2x+y)=m-1+4m+1$
$\Leftrightarrow 4x=5m$
$\Leftrightarrow x=\frac{5m}{4}$
$y=2x-(m-1)=\frac{5m}{2}-(m-1)=\frac{3m+2}{2}$
Khi đó:
$2x^2-3y=2$
$\Leftrightarrow \frac{25m^2}{8}-\frac{3(3m+2)}{2}=2$
$\Leftrightarrow 25m^2-36m-40=0$
$\Leftrightarrow m=\frac{18\pm 2\sqrt{331}}{25}$