Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

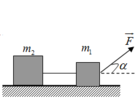
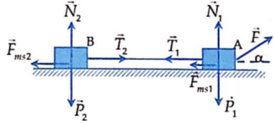
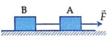
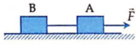
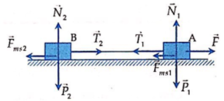
Phân tích các lực tác dụng lên hệ vật
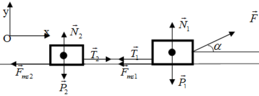
Chọn hệ quy chiếu như hình vẽ như hình vẽ, chiều dương (+) là chiều chuyển động
Xét vật 1 : Áp dụng định luật II Newton ta có
F → + F → m s 1 + N → + P → + T → 1 = m 1 a →
Chiếu lên Ox: F cos α − F m s 1 − T 1 = m 1 a
Chiếu lên Oy: N 1 − P 1 + F sin α = 0 ⇒ N 1 = m 1 g − F sin α
Thay vào (1) ta được:
F cos α − μ m 1 g − F sin α − T 1 = m 1 a
Tương tự đối với vật 2: F → m s 2 + N → 2 + P → 2 + T → 2 = m 2 a →
Chiếu lên Ox: − F m s 2 + T 2 = m 2 a
Chiếu lên Oy: N 2 = P 2 = m 2 g
Thay vào (2) ta được − μ m 2 g + T 2 = m 2 a
Vì dây không dãn nên T = T 1 = T 2
F cos α − μ m 1 g − F sin α − T 1 = m 1 a − μ m 2 g + T 2 = m 2 a
Cộng vế ta có :
F cos α − μ m 1 g − F sin α − μ m 2 g = ( m 1 + m 2 ) a
⇒ a = F cos α − μ ( m 1 g − F sin α ) − μ m 2 g ( m 1 + m 2 )
⇒ a = 10. cos 30 0 − 0 , 1 3.10 − 10. sin 30 0 − 0 , 1.2.10 3 + 2 = 0 , 832 m / s 2
Thay vào (**) ta có
T =...

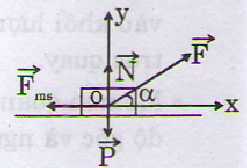
Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


Chọn C.
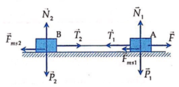
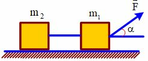
Áp dụng định luật II Niu-tơn cho hệ vật:
F – Fms1 – Fms2 = (m1 + m2).a
Dễ thấy: N1 = P1; N2 = P2
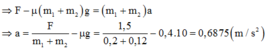
Áp dụng định luật II Niu-tơn cho vật B:
T – μm2.g = m2.a ⟹ T = (μg + a).m2 = 0,5625 N

Chọn B.
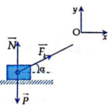
Áp dụng định luật II Niu-tơn:
![]()
Chiếu lên Oy: N = P – F.sinα
Chiếu lên Ox: F.cosα – μN = m.a
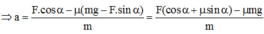
Theo Bất đẳng thức Bu-nhi-a - Cốp-xki:
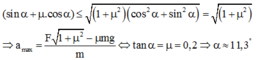

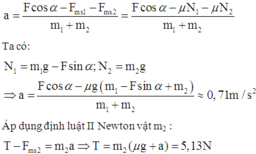


Chọn đáp án B
+ Chọn hệ quy chiếu như hình vẽ, chiều dương (+) là chiều chuyển động
Xét vật 1: Áp dụng định luật II Niwton ta có:
+ Chiếu lên Ox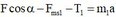 (1)
(1)
+ Chiếu lên Oy:
Xét vật 2
+ Chiếu lên Ox: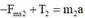 (2)
(2)
+ Chiếu lên Oy:
+ Vì dây không dãn nên:
+ Từ (*) và (**):
+ Cộng vế ta có:
a=0,832
+ Thay vào (**):