Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

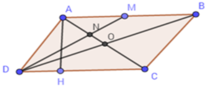
a) Gọi H là chân đường vuông góc kẻ từ A xuống CD
Theo đề bài, ta có: AH=3(cm)
Xét hình bình hành ABCD có AH là đường cao ứng với cạnh CD(gt)
nên \(S_{ABCD}=AH\cdot CD=4\cdot3=12\left(cm^2\right)\)

Giải thích các bước giải:
Gọi AH là đg cao từ A xuống cạnh CD
a, diện h hbh=AHxCD=12.16=192
b,M trung điểm AB nên AM=16:2=8cm
vì ABCD là hbh nên đường cao từ D xuống AB= AH=12cm
do đó diện tích tam giác ADM=12x8:2=48
c, Xét tam giác ANM và CND
vì AM//CD nên CDAM=DNMN=12CDAM=DNMN=12 suy ra DN=2NM
d, vì DN=2NM nên chiều cao từ D xuống AM = 3 từ N xuống AM=> chiều cao từ N xuống AM=12:3=4cm
suy ra diện tích AMN=AMx4:2=16

SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A