Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

......................?
mik ko biết
mong bn thông cảm
nha ................

a, hàm số đi qua gốc tọa độ O
\(\Rightarrow\) đồ thị hàm số có dạng \(y=x.z=mx+(2m+1)\Rightarrow 2m+1=0\)
\(\Rightarrow m=-\dfrac{1}{2}\)
b, khi \(m=1\Rightarrow y=x+3\)
Xét y=0 suy ra x=-3
suy ra lấy điểm A(-3,0)
Xét x=0 suy ra y=3
Lấy điểm B(0,3)
Nối A,B ta được đồ thị cần vẽ
y x o -3 3 y=+3
c, đồ thị hàm số trên cắt đồ thị hàm số y=2x-1 tại 1 điểm trên trục tung suy ra gọi điểm đó là M ta có ( giao của 2 đồ thị nha)
M có hoành độ =0
thay vào 2 hàm số trên suy ra:
\(\hept{\begin{cases}y=2m+1\\y=-1\end{cases}\Rightarrow2m+1=-1\Rightarrow m=-1}\)
Xong rồi bạn nha!

a: Thay x=0 và y=2 vào (d), ta được:
\(0\left(m-1\right)+m=2\)
=>m+0=2
=>m=2
b: Thay x=-3 vào y=0 vào (d), ta được:
\(-3\left(m-1\right)+m=0\)
=>-3m+3+m=0
=>-2m+3=0
=>-2m=-3
=>\(m=\dfrac{3}{2}\)
c: Khi m=2 thì (d): \(y=\left(2-1\right)x+2=x+2\)
Khi m=3/2 thì (d): \(y=\left(\dfrac{3}{2}-1\right)x+\dfrac{3}{2}=\dfrac{1}{2}x+\dfrac{3}{2}\)
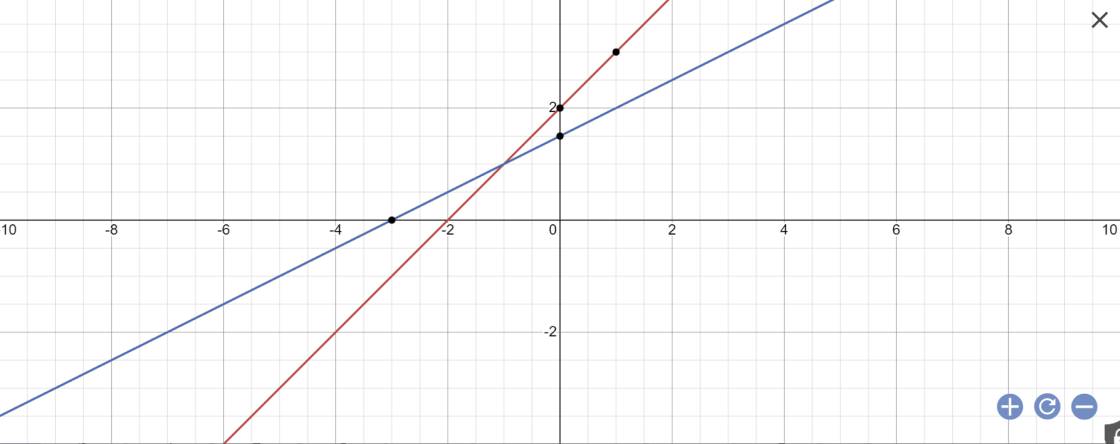
Tọa độ giao điểm của hai đường thẳng này là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+2=\dfrac{1}{2}x+\dfrac{3}{2}\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-\dfrac{1}{2}x=\dfrac{3}{2}-2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=-\dfrac{1}{2}\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-1+2=1\end{matrix}\right.\)

a, Để y là hàm số bậc nhất thì \(m+5\ne0\Leftrightarrow m\ne-5\)
b, Để y là hàm số đồng biến khi \(m+5>0\Leftrightarrow m>-5\)
c, Thay x = 2 ; y = 3 vào hàm số y ta được :
\(2\left(m+5\right)+2m-10=3\)
\(\Leftrightarrow4m=3\Leftrightarrow m=\frac{3}{4}\)
d, Do đồ thị cắt trục tung tại điểm có hoành độ bằng 9 => y = 9 ; x = 0
Thay x = 0 ; y = 9 vào hàm số y ta được :
\(2m-10=9\Leftrightarrow m=\frac{19}{2}\)
e, Do đồ thị đi qua điểm 10 trên trục hoành => x = 10 ; y = 0
Thay x = 10 ; y = 0 vào hàm số y ta được :
\(10m+50+2m-10=0\Leftrightarrow12m=-40\Leftrightarrow m=-\frac{40}{12}=-\frac{10}{3}\)
f, Ta có : y = ( m + 5 )x + 2m - 10 => a = m + 5 ; b = 2m - 10 ( d1 )
y = 2x - 1 => a = 2 ; y = -1 ( d2 )
Để ( d1 ) // ( d2 ) \(\Rightarrow\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}\Leftrightarrow\hept{\begin{cases}m=-3\\2m\ne9\end{cases}\Leftrightarrow}\hept{\begin{cases}m=-3\left(tm\right)\\m\ne\frac{9}{2}\end{cases}}}\)
g, h cái này mình quên rồi, xin lỗi )):
với mọi m thì hàm số trên đều là hàm số bậc nhất