Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x1 = x2 + 2 (1)
Theo Viet:
x1 + x2 = -2(m - 1) (2)
x1 . x2 = m2 -4m -3 (3)
Từ (1) thay x1 vào (2) ta có:
2.x2 = 2m - 4 => x2 = m - 2
=> x1 = x2 + 2 = m
Thay x1, x2 vào (3) ta có:
m(m - 2) = m2 - 4m -3
=> 2m = -3 => m = -3/2
Thử lại Với m = -3/2 thì y = x2 - 5x + 21/4
Phương trình x2 - 5x + 21/4 = 0 có 2 nghiện là -3/2 và -7/2
x1 = x2 + 2 (1)
Theo Viet:
x1 + x2 = -2(m - 1) (2)
x1 . x2 = m2 -4m -3 (3)
Từ (1) thay x1 vào (2) ta có:
2.x2 = 2m - 4 => x2 = m - 2
=> x1 = x2 + 2 = m
Thay x1, x2 vào (3) ta có:
m(m - 2) = m2 - 4m -3
=> 2m = -3 => m = -3/2
Thử lại Với m = -3/2 thì y = x2 - 5x + 21/4
Phương trình x2 - 5x + 21/4 = 0 có 2 nghiện là -3/2 và -7/2

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-1}{2}\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{1^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{1+8}{4}=-\dfrac{9}{4}\end{matrix}\right.\)
Vì (P): \(y=x^2+x-2\) có a=1>0
nên (P) đồng biến khi x>-1/2 và nghịch biến khi x<-1/2
Vẽ (P): 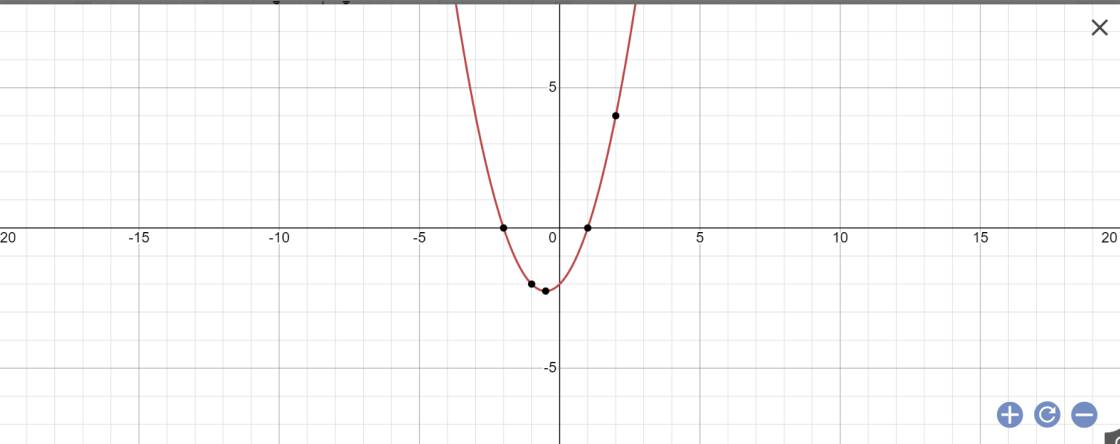
b: Phương trình hoành độ giao điểm là:
\(x^2+x-2=-\left(m+1\right)x+m+2\)
=>\(x^2+x-2+\left(m+1\right)x-m-2=0\)
=>\(x^2+\left(m+2\right)x-m-4=0\)(1)
Để (P) cắt (d) tại hai điểm phân biệt A,B nằm về hai phía so với trục Oy thì phương trình (1) có hai nghiệm phân biệt trái dấu
=>-m-4<0
=>-m<4
=>m>-4
mà \(m\in Z;m\in\left[-10;4\right]\)
nên \(m\in\left\{-3;-2;-1;0;1;2;3;4\right\}\)
=>Có 8 số thỏa mãn

Phương trình hoành độ giao điểm của (P ) và trục hoành:
x2+ 3x+m=0 (1)
+ Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt
![]()
Chọn D.

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2
