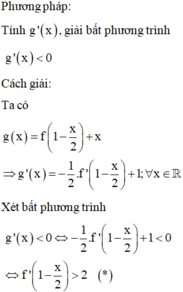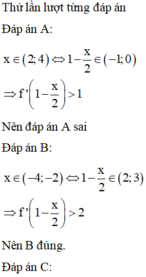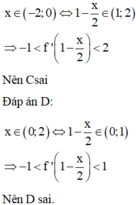Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
Bảng biến thiên :
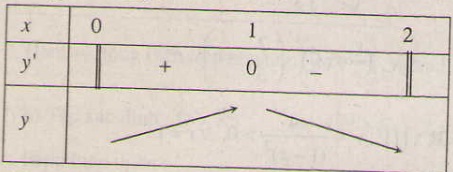
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).

+TXĐ: X\(\in\)R
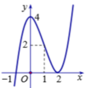
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

Chọn A.
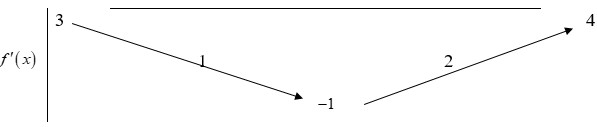
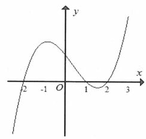
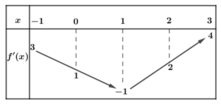
Tập xác định của hàm số y=f(x) là D=R Từ đồ thị đã cho ta có: f ' ' x = 0 ⇔ x = - 1 x = 2 .
Bảng biến thiên.
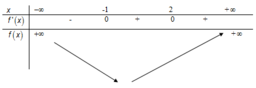
Dựa vào bảng biến thiên của hàm số y=f(x) ta nhận thấy hàm số y=f(x) đồng biến trên khoảng
-
1
;
+
∞
.

Tập xác định : D = R. y' = => y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
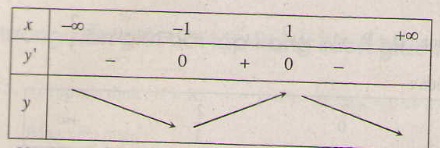
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).

Chọn đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên (a;b) có y’>0 với x thuộc (a;b) thì hàm số đồng biến trên (a;b).
Cách giải
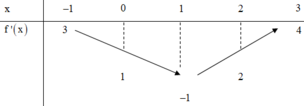
Từ BBT ta có hàm số đồng biến trên các khoảng (-∞;-1) và (0;1).

Hàm số nghịch biến nếu f’(x)<0 Quan sát đồ thị y=f’(x), chọn đáp án A. Chọn A

Ta có ![]()
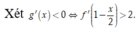
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 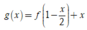 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.