Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.


Đáp án C
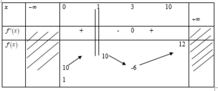
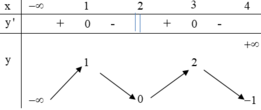
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
BBT:
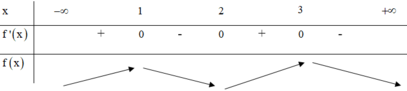
Từ BBT ta thấy (I) đúng, (II) sai.
Với ![]() => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng

Đáp án B.
Ta có: Tập xác định của hàm số y = x 2 3 + 2017 là R nên y ' = 2 3 x 3
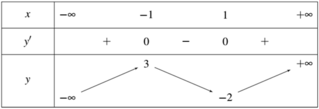
Ta có bảng biến thiên
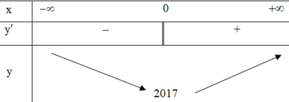
(I) sai vì hàm số chỉ đồng biến trên 0 ; + ∞ ;
(II) đúng là hàm số đạt cực tiểu x = 0; EM NHÌN KĨ BẢNG BIẾN THIÊN NHÉ!
(III) sai vì giá trị nhỏ nhất của hàm số là 2017
(IV) sai vì hàm số nghịch biến trên − ∞ ; 0
Lỗi sai
Ø Có bạn sẽ nhìn nhanh và nhầm y ' = 2 3 x 3 > 0 và kết luận là I đúng
Ø Có bạn sẽ không xét tại x = 0 vì tại đó y' không xác định. Hàm số vẫn đạt cực tiểu tại x = 0. Ta xét các điểm cực trị làm y' = 0 hoặc y' không xác định.

Chọn đáp án B
Phương pháp
Dựa vào đồ thị hàm số xác định các khoảng đơn điệu, các điểm cực trị và GTLN, GTNN của hàm số.
Cách giải
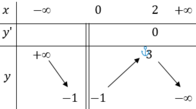
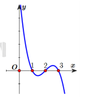
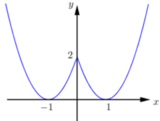
Dựa vào đồ thị hàm số ta thấy hàm số đã cho
+) Đồng biến trên (-1;0) và (1;+∞), nghịch biến trên (-∞;-1) và (0;1).
+) Hàm số có 3 điểm cực trị.
+) Hàm số không có GTLN.
Do đó các mệnh đề (I), (III) đúng.

Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng

Đáp án D
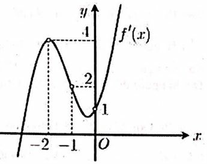
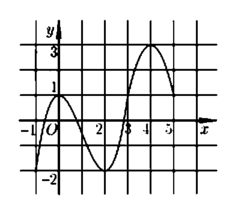
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
 Xét các khẳng định sau:
Xét các khẳng định sau: 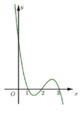



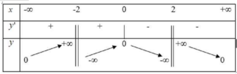
Đáp án C
A sai vì hàm số chỉ đạt cực trị tại x = 2.
B sai vì trên (0; 2) hàm số đồng biến.
C đúng vì hàm số chỉ đạt cực trị tại x = 2
D sai vì l i m x → + ∞ = + ∞ nên hàm số không có giá trị lớn nhất.