Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a, \(2y.\left(y-\dfrac{1}{7}\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}2y=0\\y-\dfrac{1}{7}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=0\\y=\dfrac{1}{7}\end{matrix}\right.\)
Vậy \(y\in\left\{0;\dfrac{1}{7}\right\}\)
b, \(\dfrac{-2}{5}+\dfrac{2}{3}y+\dfrac{1}{6}y=\dfrac{-4}{15}\)
\(\Rightarrow\dfrac{5}{6}y=\dfrac{-4}{15}+\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{6}y=\dfrac{2}{15}\)
\(\Rightarrow y=\dfrac{4}{25}\)
Vậy \(y=\dfrac{4}{25}\)
Chúc bạn học tốt!!!
Bài 1:
a, \(2y\left(y-\dfrac{1}{7}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2y=0\\y-\dfrac{1}{7}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=0\\y=\dfrac{1}{7}\end{matrix}\right.\)
Vậy...
b, \(\dfrac{-2}{5}+\dfrac{2}{3}y+\dfrac{1}{6}y=\dfrac{-4}{15}\)
\(\Rightarrow\dfrac{5}{6}y=\dfrac{2}{15}\)
\(\Rightarrow y=\dfrac{4}{25}\)
Vậy...
Bài 2:
a, \(x\left(x-\dfrac{4}{7}\right)>0\)
\(\Rightarrow\left\{{}\begin{matrix}x>0\\x-\dfrac{4}{7}>0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x< 0\\x-\dfrac{4}{7}< 0\end{matrix}\right.\)
\(\Rightarrow x>\dfrac{4}{7}\left(x\ne0\right)\) hoặc \(x< \dfrac{4}{7}\left(x\ne0\right)\)
Vậy...
Các phần còn lại tương tự nhé

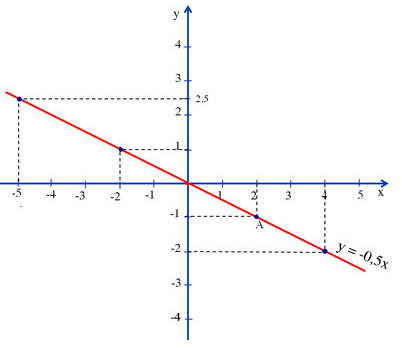
Cho x =2 được y =-2 =>A(2 ;-1) thuộc đồ thị. Vẽ đồ thị
a) Trên đồ thị ta thấy
f(2)=-1
f(-2) =1
f(4)=-2
f(0)=0;
b) Trên đồ thị ta thấy
y=-1 => x=2
y=0 => x=0
y=2,5 => x=-5
c) Khi y dương y > 0 ứng với phần đồ thị nằm trên trục hoành và bên trái trục tung nên x < 0.
Khi y âm : y < 0 ứng với phần đồ thị nằm trên trục hoành và bên phải trục tung nên x > 0

Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
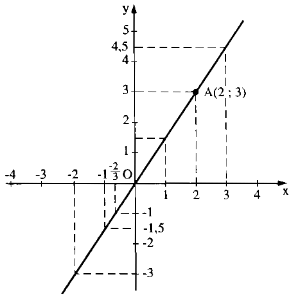
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) =0
b)\(y=-1\Rightarrow x=\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
\(y=0\Rightarrow x=\dfrac{0}{1,5}=0\)
\(y=4,5\Rightarrow x=\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.

a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) = 0
b)y=−1⇒x=\(\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
b)y=0⇒x==\(\dfrac{0}{1,5}=0\)
y=4,5⇒x=\(\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0

Nhiều quá, từng bài 1 nhé, bài nào làm được, tớ sẽ cố gắng.
bài 2:
a) \(x>2x\Leftrightarrow x-2x>0\Leftrightarrow-x>0\Leftrightarrow x< 0\)
Kl: x<0
b) \(a+x< a\Leftrightarrow x< 0\)
Kl: x<0
c) \(x^3>x^2\Leftrightarrow x^3-x^2>0\Leftrightarrow x^2\left(x-1\right)>0\) (*)
Mà x^2 > 0 \(\Rightarrow\) (*) \(\Leftrightarrow x-1>0\Leftrightarrow x>1\)
Kl: x>1
Câu 4:
a) \(1-2x< 7\Leftrightarrow2x>-6\Leftrightarrow x>3\)
Kl: x>3
b) \(\left(x-1\right)\left(x-2\right)>0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1>0\\x-2>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1< 0\\x-2< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>1\\x>2\end{matrix}\right.\\\left\{{}\begin{matrix}x< 1\\x< 2\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x>2\\x< 1\end{matrix}\right.\)
Kl: x>2 hoặc x<1
c) \(\left(x-2\right)^2\left(x+1\right)\left(x+4\right)< 0\Leftrightarrow\left(x+1\right)\left(x+4\right)< 0\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+1>0\\x+4< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+1< 0\\x+4>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-1\\x< -4\end{matrix}\right.\\\left\{{}\begin{matrix}x< -1\\x>-4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}-1< x< -4\left(vô-lý\right)\\-4< x< -1\end{matrix}\right.\) \(\Leftrightarrow-4< x< -1\)
Kl: -4<x<-1
d) ĐK: x khác 9\(\dfrac{x^2\left(x+3\right)}{x-9}< 0\Leftrightarrow x^2\left(x+3\right)\left(x-9\right)< 0\Leftrightarrow\left(x+3\right)\left(x-9\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3>0\\x-9< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\x-9>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-3\\x< 9\end{matrix}\right.\\\left\{{}\begin{matrix}x< -3\\x>9\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}-3< x< 9\left(N\right)\\9< x< -3\left(vô-lý\right)\end{matrix}\right.\) \(\Leftrightarrow-3< x< 9\)
Kl: -3<x<9
e) Đk: x khác 0
\(\dfrac{5}{x}< 1\Leftrightarrow\dfrac{5}{x}< \dfrac{5}{5}\Leftrightarrow x>5\left(N\right)\)
KL: x >5
f) ĐK: x khác 1
\(\dfrac{2x-5}{x-1}< 0\Leftrightarrow\left(2x-5\right)\left(x-1\right)< 0\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x-5>0\\x-1< 0\end{matrix}\right.\\\left\{{}\begin{matrix}2x-5< 0\\x-1>0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>\dfrac{5}{2}\\x< 1\end{matrix}\right.\\\left\{{}\begin{matrix}x< \dfrac{5}{2}\\x>1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{5}{2}< x< 1\left(vô-lý\right)\\1< x< \dfrac{5}{2}\left(N\right)\end{matrix}\right.\)
Kl: 1< x< 5/2

a)
Với A=0
\(\Rightarrow x\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}}\)
với A<0
\(\Rightarrow x\left(x-4\right)< 0\)
\(th1\orbr{\begin{cases}x< 0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x>4\end{cases}\Leftrightarrow4< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x>0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x< 4\end{cases}\Leftrightarrow0< x< 4\left(tm\right)}\)
\(\Leftrightarrow0< x< 4\Leftrightarrow x\in\left\{1;2;3\right\}\)
Với A>0
\(\Rightarrow x\left(x-4\right)>0\)
\(th1\orbr{\begin{cases}x>0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x>4\end{cases}}\Leftrightarrow x>4\)
\(th2\orbr{\begin{cases}x< 0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x< 4\end{cases}}\Leftrightarrow x< 0\)
b)
Với B=0
\(\Rightarrow\frac{x-3}{x}=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\Rightarrow x=3\\x=0\left(l\right)\end{cases}}\)
vậy x=3 thì B = 0
Với B < 0
\(\Rightarrow\frac{x-3}{x}< 0\)
\(th1\orbr{\begin{cases}x-3>0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x< 0\end{cases}\Leftrightarrow3< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x-3< 0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x>0\end{cases}\Leftrightarrow0< x< 3\left(tm\right)\Leftrightarrow x\in\left\{1;2\right\}}\)
Với B > 0
\(th1\orbr{\begin{cases}x-3>0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x>0\end{cases}\Leftrightarrow x>3}\)
\(th2\orbr{\begin{cases}x-3< 0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 0\end{cases}\Leftrightarrow x< 0}\)

\(A=2x^2\left(x-3\right)-x\left(x-3\right)\)
\(=\left(x-3\right)\left(2x^2-x\right)\)
\(=\left(x-3\right)x\left(2x-1\right)\)
Ta có:\(\left|x\right|=4\Rightarrow x=4\left(h\right)x=-4\)
Nếu x=4 thì \(A=\left(4-3\right)4\left(2\cdot4-1\right)=28\)
Nếu \(x=-4\) thì \(A=\left(-4-3\right)\left(-4\right)\left[2\left(-4\right)-1\right]=-252\)
Để \(A=0\) thì \(\left(x-3\right)x\left(2x-1\right)=0\)
\(\Leftrightarrow x-3=0\left(h\right)x=0\left(h\right)2x-1=0\)
\(\Leftrightarrow x=3\left(h\right)x=0\left(h\right)x=\frac{1}{2}\)
Mọi x>3 thì ta luôn có:\(x-3>0;x>0;2x-1>2\cdot3-1=5>0\)
\(\Rightarrow A=\left(x-3\right)x\left(2x-1\right)>0\Rightarrowđpcm\)
Để hàm số y = f (x) = -\(\dfrac{2}{3}\)x nhận giá trị dương thì x < 0