Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Hàm số ĐB\(\Leftrightarrow\) a \(>\)0
\(\Leftrightarrow\) m-2 \(>\)0 \(\Leftrightarrow\) m \(>\)2
Vậy m\(>\)2 thì hàm số ĐB.
b,ĐTHS (*) // vs đt y=2x-1 \(\Leftrightarrow\)\(\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}m-2=2\\2m+1\ne-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=4\left(tm\right)\\m\ne-1\end{cases}}\)
Vậy m=4;m\(\neq\)-1 thì ĐTHS (*) // vs đt y=2x-1
c,Gọi A(\(x_0;y_0\)) là điểm cố định mà ĐTHS (*) luôn đi qua vs mọi m
Thay x=\(x_0\) ,y=\(y_0\) vào pt đt (*) ta đc̣:
\(y_0=\left(m-2\right)x_02m+1\)\(\Leftrightarrow\)\(mx_0-2x_0+2m+1-y_0=0\)
\(\Leftrightarrow m\left(x_0+2\right)-2x_0+1-y_0=0\left(1\right)\)
Để đt (*) luôn đi qua A vs mọi m thì pt (1) luôn đúng vs mọi m ( pt (1) có vô số nghiệm m)
Điều này xảy ra \(\Leftrightarrow\hept{\begin{cases}x_0+2=0\\-2x_0+1-y_0=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_0=-2\\y_0=5\end{cases}}\)
\(\Rightarrow A\left(-2;5\right)\)
Vậy A(-2;5) là điểm cố định mà ĐTHS (*) luôn luôn đi qua vs mọi m

a) Để hàm số y = (2m - 3)x - 1 // với đường thẳng y = -5x + 3
<=> \(\hept{\begin{cases}2m-3=-5\\-1\ne3\end{cases}}\)<=> 2m = -2 <=> m = -1
b) Hàm số y = (2m - 3)x - 1 đi qua điểm A(-1; 0) => x = -1 và y = 0
Do đó: 0 = (2m - 3).(-1) - 1 = 0 <=> 3 - 2m = 1 <=> 2m = 2 <=> m = 1
Vậy để đò thị hàm số đi qua A(-1; 0) <=> m = 0
c) Gọi tọa độ gđ của 3 đường thẳng y = (2m- 3 )x - 1 , y = 1 và y = 2x - 5 là (x0; y0)
Do đó: \(\hept{\begin{cases}y_0=\left(2m-3\right)x_0-1\\y_0=1\\y_0=2x_0-5\end{cases}}\) <=> \(\hept{\begin{cases}1=\left(2m-3\right)x_0-1\\2x_0-5=1\end{cases}}\)
<=> \(\hept{\begin{cases}\left(2m-3\right)x_0=2\\2x_0=6\end{cases}}\) <=> \(\hept{\begin{cases}\left(2m-3\right).3=2\\x_0=3\end{cases}}\) <=> 2m - 3 = 2/3 <=> 2m = 11/3 <=> m = 11/6
Vậy m = 11/6 thì đồ thị hàm số đã cho và các đường thẳng y = 0 và y = 2x - 5 đồng quy tại 1 điểm



h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)
Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
y=x+4
=>x-y+4=0
Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)
=>\(m\ne2\)
b: Để (1) đồng biến thì m-2>0
=>m>2
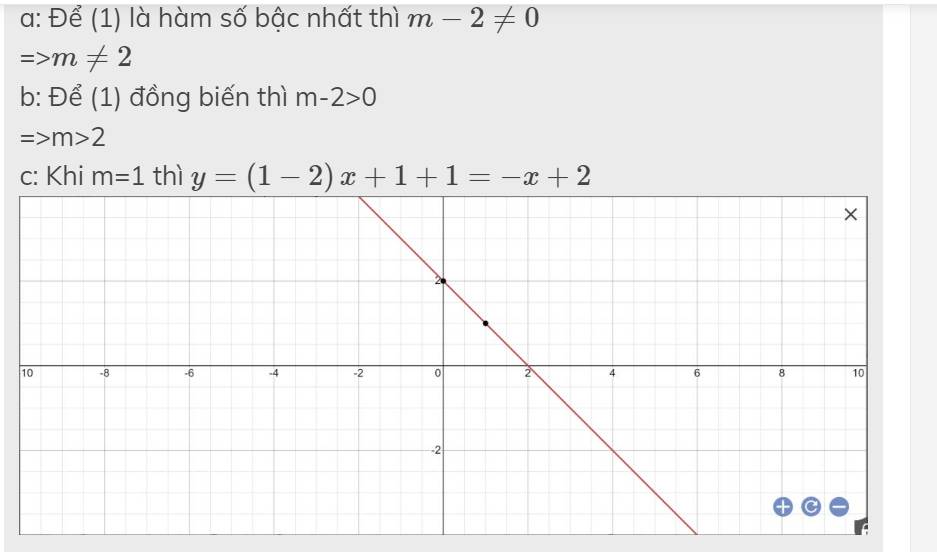
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)
d: Thay x=2 và y=1 vào (1), ta được:
\(2\left(m-2\right)+m+1=1\)
=>2m-4+m=0
=>3m-4=0
=>3m=4
=>\(m=\dfrac{4}{3}\)
e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)
=>m=3
f: Để (1) tạo với trục Ox một góc tù thì m-2<0
=>m<2
g: Thay x=0 vào y=5x+6, ta được:
\(y=5\cdot0+6=6\)
Thay x=0 và y=6 vào (1), ta được:
\(0\left(m-2\right)+m+1=6\)
=>m+1=6
=>m=5

a) y=(m-1)x+m+3 (d1) (a=m-1;b=m+3)
y=-2x+1 (d2) (a' =-2;b' =1)
vì hàm số (d1) song song với hàm số (d2) nên
\(\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\Leftrightarrow\hept{\begin{cases}m-1=-2\\m+3\ne1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=-1\\m\ne-2\end{cases}}\)
vậy với m= -1 thì hàm số (d1) song song với hàm số (d2)
b) vì hàm số (d1) đi qua điểm (1;-4) nên
x=1 ; y= -4
thay vào (d1) ta có
-4=m-1+m+3 (mình làm tắt ko nhân với 1 nha)
-4=2m+2
-2=2m
m=-1
