Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: △ ⊥ d △ ⊥ A B ⇒ u △ → = u d → ; A B →
Viết phương trình đường thẳng biết điểm đi qua và VTCP.
Cách giải: d; x + 1 - 2 = y - 2 1 = z - 3 3 có 1 VTCP u → - 2 ; 1 ; 3 ; A B → = - 2 ; 3 ; 2
∆ vuông góc với d và AB => AB nhận u → - 2 ; 1 ; 3 và A B → = - 2 ; 3 ; 2 là cặp VTPT
=> ∆ có 1 VTCP v → = A B → ; u → = ( 7 ; 2 ; 4 )
Phương trình đường thẳng ∆: x - 1 7 = y + 1 2 = z - 1 4

Đáp án B
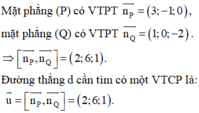
Vì A 1 ; 1 ; − 2 ∈ d nên phương trình của đường thẳng d là: x = 1 + 2 t y = 1 + 6 t z = − 2 + t

Đáp án D
Ta có y = a x 4 + b x 2 + 2 → y ' = 4 a x 3 + 2 b x ⇒ y ' 1 = − 4 a − 2 b .
Theo bài ra, ta có y ' − 1 = − 2 y − 1 = 1 ⇔ − 4 a − 2 b = − 2 a + b + 2 = 1 ⇔ a = 2 b = − 3 ⇒ a 2 − b 2 = − 5.

Đáp án D.
Do A − 1 ; 1 thuộc đồ thị hàm số nên: 1 = a + b + 2 ⇔ a + b = − 1 (1).
Tiếp tuyến tại điểm A − 1 ; 1 vuông góc với đường thẳng d : x − 2 y + 3 = 0 ⇒ y ' − 1 . k d = − 1.
Trong đó:
k d = 1 2 ; y ' = 4 a x 3 + 2 b x ⇒ y ' − 1 = − 4 a − 2 b
Suy ra :
− 4 a − 2 b . 1 2 = − 1 ⇔ 2 a + b = 1 2
Từ (1) và (2) suy ra a = 2 b ; b = − 3 ⇒ a 2 − b 2 = − 5.
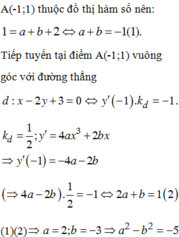


Đáp án B
Ta có y ' = 3 x 2 - 12 x + 9 = 0 ⇔ [ x = 3 ⇒ y = - 2 x = 1 ⇒ y = 2 ⇒ M 3 ; - 2 N 1 ; 2 ⇒ M N : 2 x + y - 4 = 0 .
Phương trình đường thẳng đi qua điểm A(-1;1) và vuông góc với (MN) là (d): y = 1 2 x + 3 2 .