Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=1-\dfrac{1}{\left(x-1\right)^2}\)
Tiếp tuyến d tại \(A\left(a;a+1+\dfrac{1}{a-1}\right)\) có dạng:
\(y=\left(1-\dfrac{1}{\left(a-1\right)^2}\right)\left(x-a\right)+a+1+\dfrac{1}{a-1}\)
\(\Leftrightarrow y=\dfrac{a^2-2a}{\left(a-1\right)^2}x+\dfrac{a^2}{\left(a-1\right)^2}\)
\(\Rightarrow M\left(\dfrac{a^2}{2a-a^2};0\right)\) ; \(N\left(0;\dfrac{a^2}{\left(a-1\right)^2}\right)\Rightarrow\left\{{}\begin{matrix}OM=\dfrac{a^2}{\left|2a-a^2\right|}\\ON=\dfrac{a^2}{\left(a-1\right)^2}\end{matrix}\right.\)
\(\dfrac{a^2}{\left(a-1\right)^2}=\dfrac{2a^2}{\left|2a-a^2\right|}\Leftrightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\\left|a^2-2a\right|=2\left(a^2-2a+1\right)\end{matrix}\right.\)
Đặt \(a^2-2a=t\Rightarrow\left|t\right|=2\left(t+1\right)\) (với \(t\ge-1\))
\(\Leftrightarrow\left[{}\begin{matrix}2t+2=t\\2t+2=-t\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}t=-2\left(loại\right)\\t=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow a^2-2a=-\dfrac{2}{3}\Leftrightarrow a^2-2a+\dfrac{2}{3}=0\)
Người ra đề đam mê với nghiệm xấu thì phải

- Tiếp tuyến (d) tại điểm M của đồ thị (C) có hoành độ x 0 = 0 ⇒ y 0 = 3 .
- Ta có:
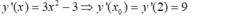
- Phương trình tiếp tuyến (d) tại điểm M của đồ thị (C) là:
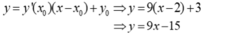
- Xét phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm phương trình :
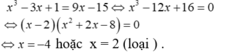
- Với x = -4 thì y = 9.(-4) – 15 = -51.
- Vậy N(- 4 ; -51) là điểm cần tìm.
Chọn C.

\(y'=\dfrac{1}{2}x^3-\dfrac{7}{2}x\)
Chỉ cần để ý 1 lý thuyết:
Đường thẳng đi qua 2 điểm \(A\left(x_1;y_1\right)\) và \(B\left(x_2;y_2\right)\) sẽ có hệ số góc \(k=\dfrac{y_1-y_2}{x_1-x_2}\)
Do đó ta có hệ số góc của đường thẳng MN là \(k=3\)
\(\Rightarrow\dfrac{1}{2}x^3-\dfrac{7}{2}x=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-1\\x=3\end{matrix}\right.\) (sao lắm nghiệm vậy trời)
Biết hoành độ 3 tiếp điểm, bạn viết 3 pt tiếp tuyến rồi xét pt hoành độ với (C) coi cái nào có 4 nghiệm (trong đó có 1 nghiệm kép) thì nhận

x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16

Chọn A.
Ta có: y’ = 3x2 – 4x + 2.
Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1
Hoành độ x1, x2 của các điểm M, N là nghiệm của phương trình 3x2 – 4x + 2 = 1.
Suy ra x1 + x2 = 4/3 ( hệ thức Vi-et).

Lời giải:
Ta có: \(y=\frac{x+2}{2x+3}\Rightarrow y'=\frac{-1}{(2x+3)^2}\)
Gọi tiếp điểm có hoành độ là $a$. Khi đó pt tiếp tuyến của $(C)$ tại tiếp điểm là:
d: \(y=f'(a)(x-a)+f(a)=\frac{-1}{(2a+3)^2}(x-a)+\frac{a+2}{2a+3}(*)\)
Từ đây ta suy ra :
\(d\cap Ox=A(2a^2+8a+6,0)\)
\(d\cap Oy=B(0, \frac{2a^2+8a+6}{(2a+3)^2})\)
Vì tam giác $OAB$ cân tại $O$ nên:
\(OA=OB\Leftrightarrow |2a^2+8a+6|=|\frac{2a^2+8a+6}{(2a+3)^2}|\)
\(\Leftrightarrow |2a^2+8a+6|\left(1-\frac{1}{(2a+3)^2}\right)=0\)
Hiển nhiên $|2a^2+8a+6|\neq 0$ do $A$ khác $O$
\(\Rightarrow 1-\frac{1}{(2a+3)^2}=0\Rightarrow (2a+3)^2=1\)
\(\Rightarrow 2a+3=\pm 1\Rightarrow a=-2; a=-1\)
Thay vào $(*)$ suy ra PTTT là:
\(\left[\begin{matrix}
y=-x\\
y=-x-2\end{matrix}\right.\)




Đáp án đúng : C