Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)
b) Tiệm cận đứng là đường thẳng \(x=3\)
Tiệm cận ngang là đường thẳng \(y=1\)
Đồ thị © có tiệm cận đứng là đường thẳng x=1 và tiệm cận ngang là đường thẳng y=2.Giao điểm của hai tiệm cận là I(1;2)
Gọi M(x0;2x0−3x0−1)∈©M(x0;2x0−3x0−1)∈©
Tiếp tuyến ΔΔ của đồ thị © tại M có phương trình
y=1(x0−1)2(x−x0)+2x0−3x0−11(x0−1)2(x−x0)+2x0−3x0−1
Giao điểm của ΔΔ với hai tiệm cận của đồ thị © là A(1;2x0−4x0−1)vàB(2x0−1;2)A(1;2x0−4x0−1)vàB(2x0−1;2)
ta có:IA=∣∣∣2x0−4x0−1−2∣∣∣=2|x0−1||2x0−4x0−1−2|=2|x0−1|
IB=2|x0−1|2|x0−1|
Do đó diện tích △IAB△IAB là: S=12IAIB=212IAIB=2
Gọi pp là nửa chu vi △IAB△IAB.Khi đó bán kính đường tròn nội tiếp △IAB△IAB là r=Spr=Sp=2p2p
rr lớn nhất khi pp nhỏ nhất
mặt khác,ta có :2p=IA+IB+AB=IA+IB+√IA2+IB2≥2√IAIB+√2IAIB=4+2√22p=IA+IB+AB=IA+IB+IA2+IB2≥2IAIB+2IAIB=4+22
Suy ra: pmin=2+√2pmin=2+2,dấu bằng xẩy ra ⇔IA=IB⇔2|x0−1|=2|x0−1|⇔[x0=0x0=2⇔IA=IB⇔2|x0−1|=2|x0−1|⇔[x0=0x0=2
với x0=0x0=0,phương trình tiếp tuyến cần tìm là Δ1Δ1:y=x+3
với x0=2x0=2,phương trình tiếp tuyến cần tìm là Δ2Δ2:y=x-1
Xét : \(M\left(x_0;x_0+1+\frac{1}{x_0+1}\right)\)
Tiếp tuyến tại M có phương trình \(y=\left(1-m^2\right)x+m^2+2m+1\) (với \(m=\frac{1}{x_0-1}\))
tiếp tuyến cắt tiệm cận đứng tại \(A\left(1;2m+2\right)\); cắt tiệm cận tại \(B\left(1+\frac{2}{m};2+\frac{2}{m}\right)\) và hai tiệm cận cắt nhau tại I(1;2)
Chu vi tam giác ABI : \(P=AB+BI+IA=\sqrt{4m^2+\frac{8}{m^2}+8}+\frac{2\sqrt{2}}{\left|m\right|}+2\left|m\right|\)
Áp dụng Bất đẳng thức Côsi, ta có :
\(4m^2+\frac{8}{m^2}\ge8\sqrt{2};\frac{2\sqrt{2}}{\left|m\right|}+2\left|m\right|\ge4\sqrt[4]{2}\Rightarrow P\ge\sqrt{8\sqrt{2}+8}+4\sqrt[4]{2}\)
Đẳng thức xảy ra \(\Leftrightarrow m=\pm\sqrt[4]{2}\)
Vậy \(M\left(1\pm\frac{1}{\sqrt[4]{2}};2\pm\frac{1}{\sqrt[4]{2}}\pm\sqrt[4]{2}\right)\)
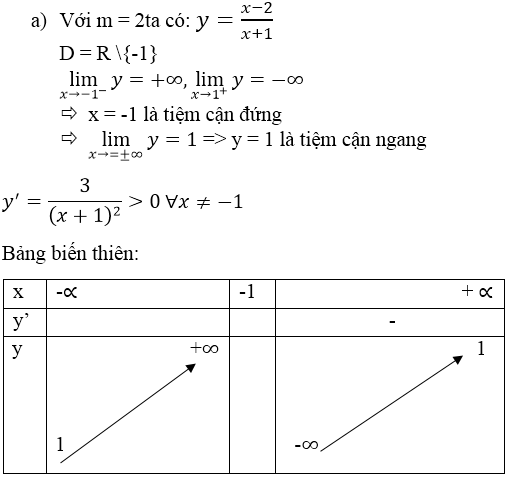
+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có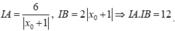
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
Suy ra,
Chọn D.