Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Để đồ thị của hàm số y=(m-1)x+m+3 song song với đồ thị hàm số y=-2x+1 thì:
\(\left\{{}\begin{matrix}m-1=-2\\m+3\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne-2\end{matrix}\right.\)
Vậy để 2 đồ thị trên song song với nhau thì m=-1 và m\(\ne\)-2
2. Vì đồ thị đi qua điểm (1;-4) nên ta có:
-4=m-1+m+3
\(\Leftrightarrow\) 2m=-6
\(\Leftrightarrow m=-3\)
Vậy để đồ thị đi qua điểm (1;-4) thì m=-3

1. vẽ hình
y ' = 2X =0 => X = 0 , tự vẽ
2. ta có hệ số góc k = Y'(2) =4
KL : K=4 THỎA YÊU CẦU ĐỀ BÀI

1) d qua A nên tọa dộ A thỏa mãn hàm số y=m+x
<=> 2010=1+m
=>m=2009
2) (d):x-y+m=0
d song song với x-y+3=0 nêm m\(\ne\)3
vậy giá trị m thỏa : m\(\ne\)3

1, bạn tự vẽ nha
2, xét pt: \(x^2=4x+m\Leftrightarrow x^2-4x-m=0\)(1) ; \(\Delta=16-4.-m=16+16m\)
(dm) và (P) cắt nhau tại hai điểm phân biệt <=> pt có 2 nghiệm p.biệt <=> \(\Delta>0\Leftrightarrow16+16m>0\Leftrightarrow m>-1\)
th1: chọn tung độ của giao điểm 1 là 1 <=> y1=1<=> \(x1=\sqrt{y1}=\sqrt{1}=1\); \(x1=\frac{4+\sqrt{16\left(m+1\right)}}{2}=\frac{4\left(1+\sqrt{m+1}\right)}{2}=2+2\sqrt{m+1}\)
thay x=1 vào ta có: \(2+2\sqrt{m+1}=1\Leftrightarrow2\sqrt{m+1}=-1\Rightarrow\)PTVN
th2: y2=1 <=> x2=1
\(x2=\frac{4-\sqrt{16\left(m+1\right)}}{2}=2-2\sqrt{m+1}\). thay x2=1 vào: \(2-2\sqrt{m+1}=1\Leftrightarrow-2\sqrt{m+1}=-1\Leftrightarrow\sqrt{m+1}=\frac{1}{2}\Leftrightarrow m+1=\frac{1}{4}\Leftrightarrow m=-\frac{3}{4}\)(t/m đk)
=> m=-3/4 thì (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó tung độ của một trong hai giao điểm đó bằng 1.

Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
![]()
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
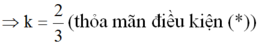
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:
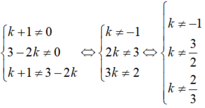
Vậy với ![]() thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)
b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5
Thay y=5 và x=0 vào hs và tìm k
2. a) Tự vẽ
b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)
c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y) (x=-2; y=0)
3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)
Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1
Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3

a, Để y là hàm số bậc nhất thì \(m+5\ne0\Leftrightarrow m\ne-5\)
b, Để y là hàm số đồng biến khi \(m+5>0\Leftrightarrow m>-5\)
c, Thay x = 2 ; y = 3 vào hàm số y ta được :
\(2\left(m+5\right)+2m-10=3\)
\(\Leftrightarrow4m=3\Leftrightarrow m=\frac{3}{4}\)
d, Do đồ thị cắt trục tung tại điểm có hoành độ bằng 9 => y = 9 ; x = 0
Thay x = 0 ; y = 9 vào hàm số y ta được :
\(2m-10=9\Leftrightarrow m=\frac{19}{2}\)
e, Do đồ thị đi qua điểm 10 trên trục hoành => x = 10 ; y = 0
Thay x = 10 ; y = 0 vào hàm số y ta được :
\(10m+50+2m-10=0\Leftrightarrow12m=-40\Leftrightarrow m=-\frac{40}{12}=-\frac{10}{3}\)
f, Ta có : y = ( m + 5 )x + 2m - 10 => a = m + 5 ; b = 2m - 10 ( d1 )
y = 2x - 1 => a = 2 ; y = -1 ( d2 )
Để ( d1 ) // ( d2 ) \(\Rightarrow\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}\Leftrightarrow\hept{\begin{cases}m=-3\\2m\ne9\end{cases}\Leftrightarrow}\hept{\begin{cases}m=-3\left(tm\right)\\m\ne\frac{9}{2}\end{cases}}}\)
g, h cái này mình quên rồi, xin lỗi )):

a/ Hai hàm số có đồ thị // với nhau khi
\(\hept{\begin{cases}m-2=1\\3\ne0\end{cases}}\Leftrightarrow m=3\)
b/ Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ
\(\hept{\begin{cases}y=x+3\\y=2x+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)
c/ Gọi điểm mà đường thẳng luôn đi qua là M(a,b) ta thế vào hàm số được
\(b=ma+3\)
\(\Leftrightarrow ma+3-b=0\)
Để phương trình này không phụ thuôc m thì
\(\hept{\begin{cases}a=0\\3-b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=0\\b=3\end{cases}}\)
Tọa độ điểm cần tìm là M(0, 3)
d/ Ta có khoản cách từ O(0,0) tới (d) là 1
\(\Rightarrow=\frac{\left|0-0m-3\right|}{\sqrt{1^2+m^2}}=\frac{3}{\sqrt{1+m^2}}=1\)
\(\Leftrightarrow\sqrt{1+m^2}=3\)
\(\Leftrightarrow m^2=8\)
\(\Leftrightarrow\orbr{\begin{cases}m=2\sqrt{2}\\m=-2\sqrt{2}\end{cases}}\)
