Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
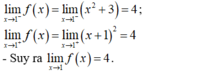
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
Chọn A

Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
![]()
suy ra ![]() .
.
Vậy để hàm số gián đoạn tại x = 1 khi ![]() ⇔ k2 ≠ 4 ⇔ k ≠ ±2.
⇔ k2 ≠ 4 ⇔ k ≠ ±2.

a) Với mọi điểm \({x_0} \in \left( {1;2} \right)\), ta có: \(f\left( {{x_0}} \right) = {x_0} + 1\).
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = {x_0} + 1\).
Vì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right) = {x_0} + 1\) nên hàm số \(y = f\left( x \right)\) liên tục tại mỗi điểm \({x_0} \in \left( {1;2} \right)\).
b) \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {x + 1} \right) = 2 + 1 = 3\).
\(f\left( 2 \right) = 2 + 1 = 3\).
\( \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right)\).
c) \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x + 1} \right) = 1 + 1 = 2\)
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k \Leftrightarrow 2 = k \Leftrightarrow k = 2\)
Vậy với \(k = 2\) thì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k\).
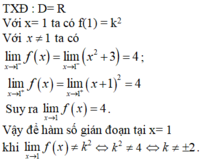
- Ta có
- Hàm số liên tục tại x = 2.