Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

a) Ta có a = 1- √5 < 0 nên hàm số đã cho nghịch biến trên R.
b) Khi x = 1 + √5 ta có:
y = (1 - √5).(1 + √5) - 1 = (1 - 5) - 1 = -5
c) Khi y = √5 ta có:
√5 = (1 - √5)x - 1
=> √5 + 1 = (1 - √5)x
![]()
(hoặc trục căn thức ở mẫu như dưới đây:
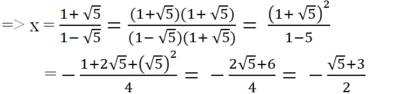

Ta có:
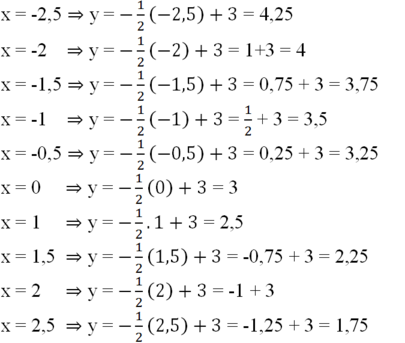
Ta được bảng sau:

b) Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.

a)
Ta thấy \(\sqrt{3}-2< 0\) nên hàm số trên nghịch biến trên R
b)
\(\sqrt{3}-7=\left(\sqrt{3}-2\right)x+5\)
\(\Leftrightarrow\sqrt{3}-12=\left(\sqrt{3}-2\right)x\)
\(\Leftrightarrow x=\dfrac{\sqrt{3}-12}{\sqrt{3}-2}\)

Cho hàm số y=(1-√5)x-1
a, Hàm số đồng biến hay nghịch biến trên R?vì sao
Hàm số nghịch biến vi (1-√5<0
b,Tính y khi x=1+√5
y=(1-√5)(1+√5)-1
y = -5

a, Vì \(1-\sqrt{5}< 0\)nên hàm nghịch biến
b, \(x=1+\sqrt{5}x\)
\(\Leftrightarrow x-x\sqrt{5}=1\)
\(\Leftrightarrow x\left(1-\sqrt{5}\right)=1\)
\(\Leftrightarrow x=\frac{1}{1-\sqrt{5}}\)
Khi đó \(y=\left(1-\sqrt{5}\right).\frac{1}{1-\sqrt{5}}-1=1-1=0\)
b, \(y=-\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x-1=-\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x=1-\sqrt{5}\)
<=> x = 1

a, Vì \(5-3\sqrt{2}>0\) nên hs đồng biến trên R
b, \(x=5+3\sqrt{2}\Leftrightarrow y=25-18+\sqrt{2}-1=6+\sqrt{2}\)
c, \(y=0\Leftrightarrow\left(5-3\sqrt{2}\right)x+\sqrt{2}-1=0\Leftrightarrow x=\dfrac{1-\sqrt{2}}{5-3\sqrt{2}}\)
\(\Leftrightarrow x=\dfrac{\left(1-\sqrt{2}\right)\left(5+3\sqrt{2}\right)}{7}=\dfrac{-2\sqrt{2}-1}{7}\)
