Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Với 
; b = 1 thì hàm số trở thành: 
- TXĐ: D = R.
- Sự biến thiên:
+ Giới hạn:
+Bảng biến thiên:
Kết luận: Hàm số đồng biến trên 
Hàm số nghịch biến trên 
Hàm số đạt cực đại tại x = 0; yCĐ = 1
Hàm số đạt cực tiểu tại 
- Đồ thị:
Với m = 2 ta có hàm số 
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
- Đồ thị :
TXĐ: D = R
Sự biến thiên:
y′ = 3 x 2 – 6x = 3x(x – 2)
y′=0 ⇔ 
Hàm số đồng biến trên mỗi khoảng (– ∞ ;0), (2;+ ∞ )
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0 ; y CĐ = y(0) = 0
Hàm số đạt cực tiểu tại x = 2; y CT = y(2) = -4.
Giới hạn: 
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2
Suy ra đồ thị có điểm uốn I(1; -2)
Bảng biến thiên:
Đồ thị:
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).
Tập xác định: D = R;
y′= 0 ⇔ 
Hàm số đồng biến trên mỗi khoảng (– ∞ ; 0), (4; + ∞ ).
Hàm số nghịch biến trên mỗi khoảng (0; 4).
Hàm số đạt cực đại tại x = 0, y CĐ = 5. Hàm số đạt cực tiểu tại x = 4, y CT = -3.
Đồ thị đi qua A(-2; -3); B(6;5).
a) Học sinh tự làm
b) Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10
y = - x + 2 x + 2
+) Tập xác định: D = R\{-2}
+) Ta có: 
Bảng biến thiên:
Hàm số nghịch biến trên các khoảng (− ∞ ; −2), (−2; + ∞ )
+) Tiệm cận đứng x = -2 vì
Tiệm cận ngang y = -1 vì
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
Với m = 2 ta được hàm số: y = 2 x - 1 2 x + 2
- TXĐ: D = R \ {-1}
- Sự biến thiên:
+ Chiều biến thiên: Theo kết quả câu a)
Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞)
+ Cực trị : Hàm số không có cực trị.
+ Tiệm cận:
⇒ đồ thị có tiệm cận đứng là x = -1.
Lại có
⇒ đồ thị có tiệm cận ngang là y = 1.
+ Bảng biến thiên:
- Đồ thị:
+ Đồ thị cắt trục hoành tại (1/2 ; 0).
+ Đồ thị cắt trục tung tại (0 ; -1/2).
+ Đồ thị nhận I(-1 ; 1) là tâm đối xứng.
Tập xác định: D = R
y′=0 ⇔ 
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y CĐ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y CT = −2
Đồ thị có hai điểm uốn:
Bảng biến thiên:
Đồ thị:
Đồ thị cắt trục hoành tại
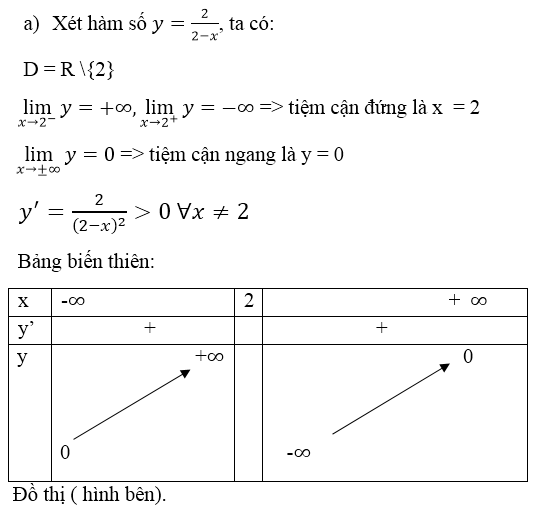
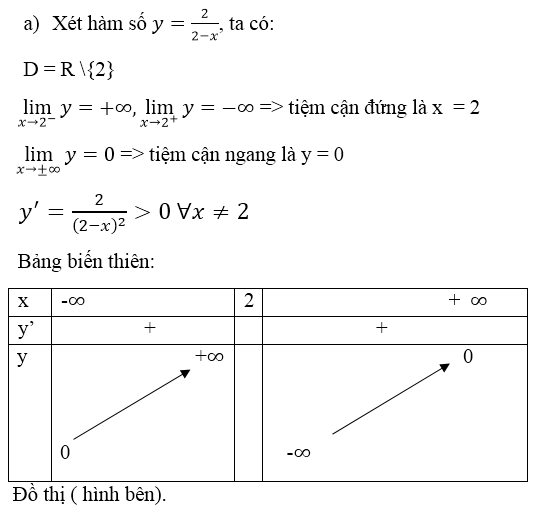
Hàm số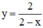
- Tập xác định: D = R\{2}
- Sự biến thiên:
⇒ Hàm số đồng biến trên (-∞; 2) và (2; +∞).
+ Cực trị : Hàm số không có cực trị
+ Tiệm cận: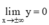
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
⇒ x = 2 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
- Đồ thị: