Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Ta có f'(x) = 3x2 + 1, g(x) = 6x + 1. Do đó
f'(x) > g'(x) <=> 3x2 + 1 > 6x + 1 <=> 3x2 - 6x >0
<=> 3x(x - 2) > 0 <=> x > 2 hoặc x > 0 <=> x ∈ (-∞;0) ∪ (2;+∞).
b) Ta có f'(x) = 6x2 - 2x, g'(x) = 3x2 + x. Do đó
f'(x) > g'(x) <=> 6x2 - 2x > 3x2 + x <=> 3x2 - 3x > 0
<=> 3x(x - 1) > 0 <=> x > 1 hoặc x < 0 <=> x ∈ (-∞;0) ∪ (1;+∞).

Ta xét bảng sau đây :
x 1 2 x-1 2 x-2 f(x) 1-x 4-2x 5-3x x-1 4-2x 3-x x-1 2x-4 3x-5
Ta có ngay với \(x\ne1\) và \(x\ne2\)
\(f'\left(x\right)=\begin{cases}-3;x< 1\\-1;1< x< 2\\3;x>2\end{cases}\)
Bây giờ xét tại \(x=1\), ta có
\(\lim\limits_{\Delta x\rightarrow0^+}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}=\lim\limits_{\Delta x\rightarrow0^+}\frac{3-\left(1+\Delta x\right)-2}{\Delta x}=\lim\limits_{\Delta x\rightarrow0^+}\frac{-\Delta x}{\Delta x}=-1\)
\(\lim\limits_{\Delta x\rightarrow0^-}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}\ne\lim\limits_{\Delta x\rightarrow0^-}\frac{5-3\left(1+\Delta x\right)-2}{\Delta x}=\lim\limits_{\Delta x\rightarrow0^-}\frac{-3\Delta x}{\Delta x}=-3\)
Như vậy \(\lim\limits_{\Delta x\rightarrow0^+}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}\ne\lim\limits_{\Delta x\rightarrow0^-}\frac{f\left(1+\Delta x\right)-f\left(1\right)}{\Delta x}\)
Nghĩa là không tồn tại đạo hàm của \(f\left(x\right)\) tại \(x=1\)
Tương tự không tồn tại đạo hàm của \(f\left(x\right)\) tại \(x=2\)

a. \(f\left(x\right)=x.e^x\)
\(f'\left(x\right)=e^x+x.e^x\)
\(f"\left(x\right)=e^x+e^x+x.e^x=2e^x+x.e^x\)
\(f^{\left(3\right)}\left(x\right)=2e^x+e^x+x.e^x=3e^x+x.e^x\)
b.Từ (a) ta đi đến công thức (dự đoán)
\(f^{\left(n\right)}\left(x\right)=ne^x+x.e^x\) (1)
Chứng minh (1) bằng quy nạp như sau :
- (1) đã đúng với \(n=1,2,3\)
- Giả sử (1) đã đúng đến n, ta phải chứng minh :
\(f^{\left(n+1\right)}\left(x\right)=\left(n+1\right)e^x+x.e^x\) (2)
Thật vậy , từ giả thiết quy nạp, ta có :
\(f^{\left(n+1\right)}\left(x\right)=\left(f^{\left(n\right)}\left(x\right)\right)'=\left(ne^x+x.e^x\right)'=ne^x+e^x+x.e^x=\left(n+1\right)e^x+x.e^x\)
Vậy (2) đúng. Theo nguyên lí quy nạp suy ra (1) đúng với mọi \(n=1,2,3....\)
Tóm lại, ta có với mọi \(n=1,2,3....\)
\(f^{\left(n\right)}\left(x\right)=ne^x+x.e^x\)

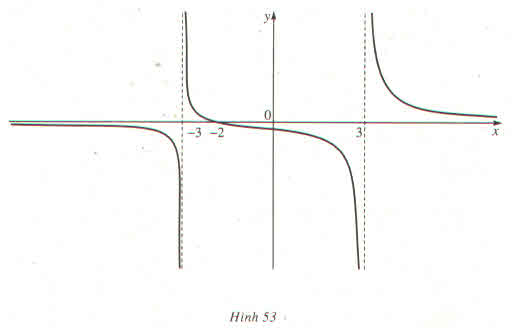
Quan sát đồ thị ta thấy x → -∞ thì f(x) → 0; khi x → 3- thì f(x) → -∞;
khi x → -3+ thì f(x) x → +∞.
b) f(x) =
=
= 0.
f(x) =
=
= -∞ vì
=
> 0 và
= -∞.
f(x) =
=
.
= +∞
vì
=
=
> 0 và
= +∞.
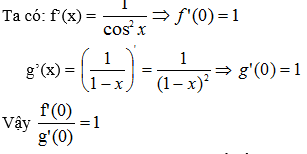
Ta có:
f(3)=√1+3=2f′(x)=12√1+x⇒f′(3)=12√1+3=14f(3)=1+3=2f′(x)=121+x⇒f′(3)=121+3=14
Suy ra:
f(3)+(x−3)f′(3)=2+x−34=5+x4
TenAnh1 TenAnh1 A = (-4.3, -9.06) A = (-4.3, -9.06) A = (-4.3, -9.06) B = (11.06, -9.06) B = (11.06, -9.06) B = (11.06, -9.06) C = (-4.3, -9.26) C = (-4.3, -9.26) C = (-4.3, -9.26) D = (11.06, -9.26) D = (11.06, -9.26) D = (11.06, -9.26) F = (10.88, -9.14) F = (10.88, -9.14) F = (10.88, -9.14)