
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3

Ta có ![]()
![]()
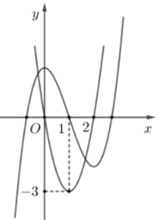
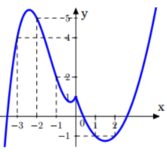
Quan sát đồ thị có 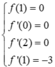
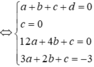

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 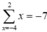
Chọn đáp án C.

Đặt ![]() khi đó yêu cầu bài toán trở thành phương trình
khi đó yêu cầu bài toán trở thành phương trình
![]() có nghiệm
t
∈
(
0
;
1
]
Có
có nghiệm
t
∈
(
0
;
1
]
Có
![]()
Do đó
![]()
![]()
![]()
Vậy ![]()
Tổng các phần tử của tập S bằng -10.
Chọn đáp án D.

Đáp án B
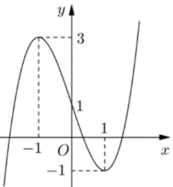
Do f 0 < 0 < f − 1 nên phương trình f x = 0 có ít nhất 1 nghiệm x ∈ − 1 ; 0
Đáp án đúng là S = ∫ − 1 1 f x d x

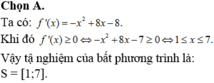


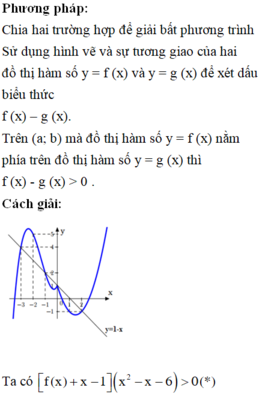

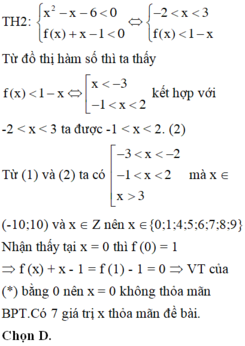
Đáp án A
Tính f ' x sau đó giải bất phương trình.
TXĐ: D = − ∞ ; 0 ∪ 1 ; + ∞
Ta có f ' x = 2 x − 1 2 x 2 − x
f ' x ≤ f x ⇔ 2 x − 1 2 x 2 − x ≤ x 2 − x
DK: x ∈ − ∞ ; 0 ∪ 1 ; + ∞
⇔ 2 x − 1 2 x 2 − x − x 2 − x ≤ 0
⇔ 2 x − 1 − 2 x 2 − x ≤ 0 ⇔ 2 x + 4 x − 1 ≤ 0
⇔ x ∈ − ∞ ; 2 − 2 2 ∪ 2 + 2 2 ; + ∞
Kết hợp điều kiện ta có: x ∈ − ∞ ; 0 ∪ 2 + 2 2 ; + ∞