Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)

\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.

y'= \(4x^3-4\left(m-1\right)x\)
Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)
\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)
Vậy \(m\in\) (−\(\infty\);2]

Ta có : \(y'=4x^3-4\left(m-1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m-1\right)x=0\Leftrightarrow x\left[x^2-\left(m-1\right)\right]=0\)
Trường hợp 1 : nếu \(m-1\le0\Leftrightarrow m\le1\), hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\), vậy \(m\le1\) thỏa mãn yêu cầu bài toán
Trường hợp 2 : nếu \(m-1>0\Leftrightarrow m>1\), hàm số đồng biến trên khoảng \(\left(-\sqrt{m-1};0\right)\) và \(\left(\sqrt{m-1};+\infty\right)\)
Để hàm số đồng biến trên khoảng (1;3) thì \(\left(\sqrt{m-1}\le1\Leftrightarrow m\le2\right)\)
Vậy hàm số đồng biến trên khoảng (1;3) \(\Leftrightarrow m\in\left(-\infty;2\right)\)

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Ta có \(y'=-\left(m-1\right)x^2+2\left(m+2\right)+3m\) \(\Rightarrow\) Hàm đồng biến trên khoảng \(\left(-\infty;-2\right)\Leftrightarrow y'\ge0,x\in\left(-\infty;-2\right)\)(*)
Vì y'(x) liên tục tại x = -2 nên (*) \(\Leftrightarrow y'\ge0;\)
và mọi x thuộc (-\(-\infty;2\) ] (*)
\(\Leftrightarrow-\left(m-1\right)x^2+2\left(m+2\right)x+3m\ge0\), mọi x thuộc (-\(-\infty;2\) ]
\(\Leftrightarrow m\left(-x^2+2x+3\right)\ge-x^2-4x\), mọi x thuộc (-\(-\infty;2\) ]\(\Leftrightarrow m\le g\left(x\right)\), mọi x thuộc (-\(-\infty;2\) ] (Trong đó \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\))
\(\Leftrightarrow m\le Min_{\left(-\infty;-2\right)}g\left(x\right)\)
Xét hàm số \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\) trên đoạn (-\(-\infty;2\) ]
\(\Rightarrow g'\left(x\right)=\frac{-6\left(x^2+x+2\right)}{\left(-x^2+2x+3\right)^2}=\frac{-6\left(x+\frac{1}{2}\right)^2+\frac{7}{4}}{\left(-x^2+2x+3\right)^2}<0\),mọi x thuộc (-\(-\infty;2\) ]
\(\Rightarrow g\left(x\right)\) là hàm số nghịch biến trên (-\(-\infty;2\) ]
\(\Rightarrow Min_{\left(-\infty;-2\right)}g\left(x\right)=g\left(-2\right)=-\frac{4}{5}\)
Vậy \(m\le-\frac{4}{5}\) thì hàm số đồng biến trên khoảng \(\left(-\infty;-2\right)\)
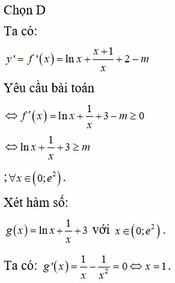

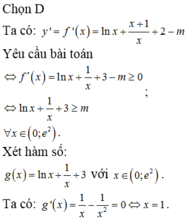
Chọn D
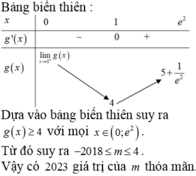
BBT :
Dựa vào BBT, hàm số đồng biến trên khoảng
So với điều kiện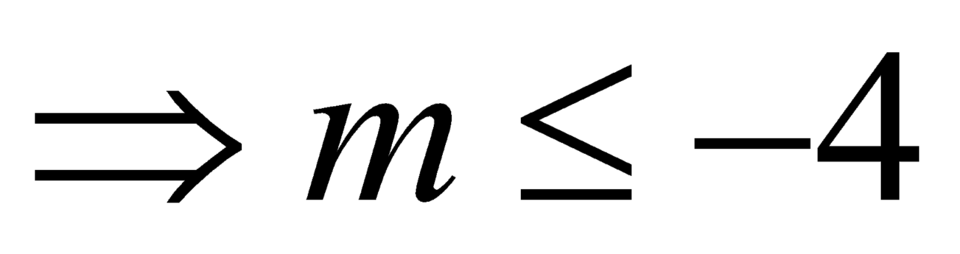 .
.
Mặt khác, theo giả thiết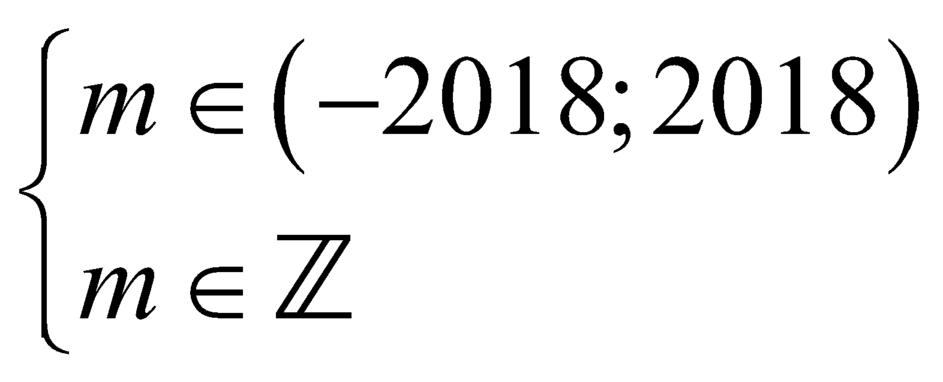
suy ra có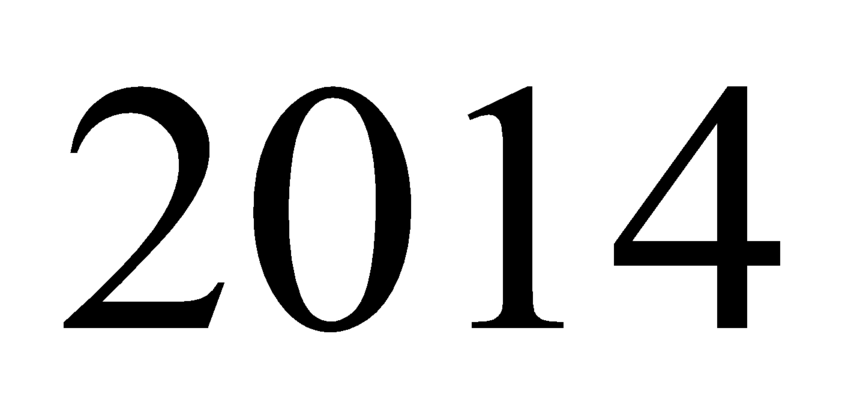 giá trị nguyên của
giá trị nguyên của 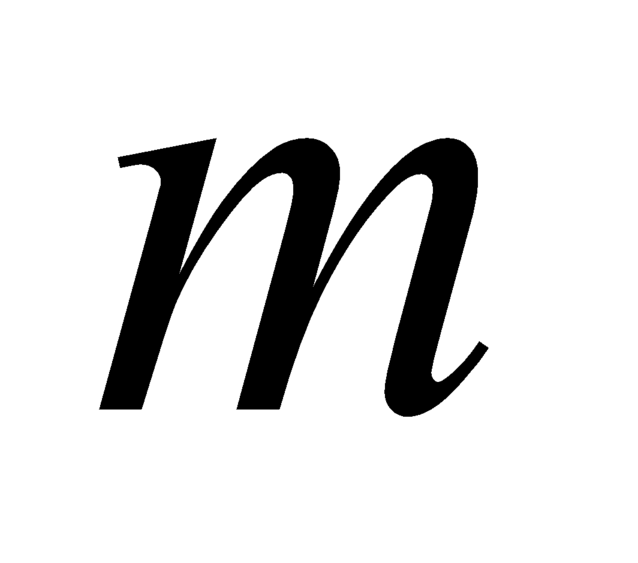 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.