Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

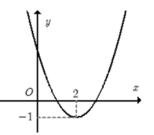
Đề là đồ thị có đỉnh là \(\left(1;2\right)\) thì hợp lí hơn
\(f\left(x\right)+m-2018=0\)
\(\Leftrightarrow f\left(x\right)=2018-m\) là phương trình hoành độ giao điểm của hai đồ thị \(y=m-2018;y=f\left(x\right)\)
Phương trình \(f\left(x\right)+m-2018=0\) có nghiệm duy nhất khi \(2018-m=2\Leftrightarrow m=2016\)
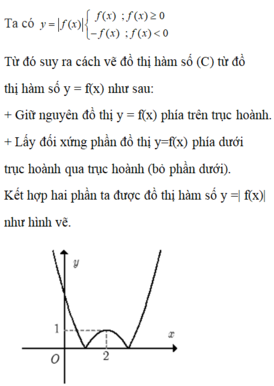
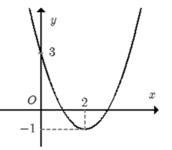
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x - 2018) - 2| = m có đúng 3 nghiệm


Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)

ai đó giúp mình với mình còn 3 tiếng nữa là tới hạn nộp bài rồi :(((