Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(x_0;y_0\right);y_0=\frac{2x_0-1}{x_0-1}\)
Phương trình tiếp tuyến \(\Delta\) của (C) tại M là :
\(y=\frac{-1}{\left(x_0-1\right)^2}\left(x-x_0+\frac{2x_0-1}{x_0-1}\right)\)
\(\Delta\) cắt tiệm cận đứng x = 1 tại A có tọa độ là nghiệm của hệ
\(\begin{cases}x=1\\y=\frac{-1}{\left(x_0-1\right)^2}\left(x-x_0+\frac{2x_0-1}{x_0-1}\right)\end{cases}\)
Do đó \(A\left(1;\frac{2x_0}{x_0-1}\right)\)

a) y=x+3x+1y=x+3x+1 có tập xác định : R\{-1}
y′=−2(x+1)2<0,∀x≠−1y′=−2(x+1)2<0,∀x≠−1
Tiệm cận đứng: x = -1
Tiệm cận ngang: y = 1
Bảng biến thiên:
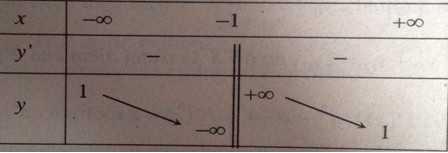
Đồ thị hàm số:
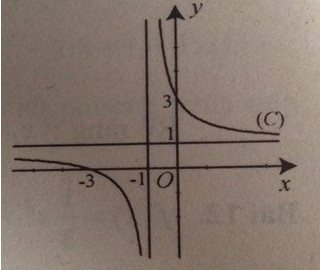
b) Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): y = 2x + m
(1)
x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1
Δ = (m+1)2 – 4.2(m-3) = m2 – 6m + 25 = (m-3)2 + 16> 0, Δm, nên (1) luôn có hai nghiệm phân biệt khác -1.
Vậy (d) luôn cắt (C) tại hai điểm phân biệt M, N (hoành độ của M, N chính là nghiệm của (1)).
TenAnh1
C = (-4.24, -6.16)
C = (-4.24, -6.16)
C = (-4.24, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
Vậy \(Min_{MN}=2\sqrt{3}\) khi \(m=3\).

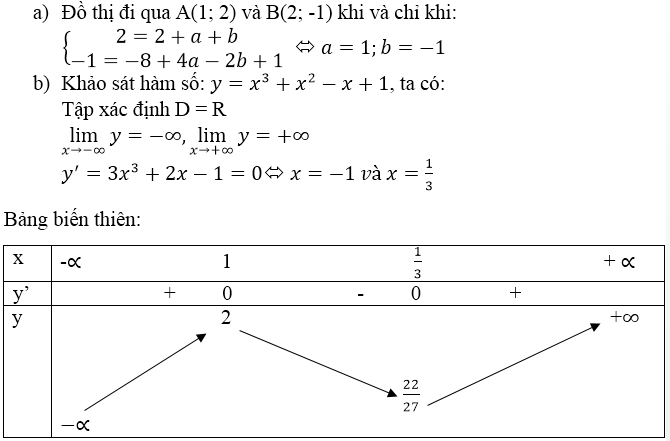
a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
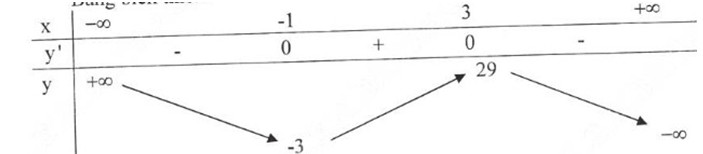
Đồ thị hàm số:
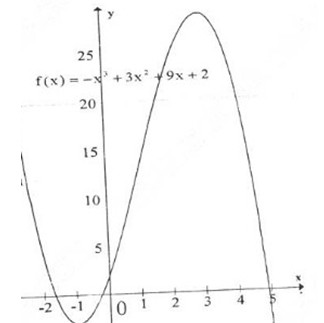
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

Với m = 1, ta có \(\left(C_1\right):y=\frac{x+1}{x-1}\)
a. Gọi d là đường thẳng đi qua P, có hệ số góc k => \(d:y=k\left(x-3\right)+1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-3\right)+1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-3\right)+1\Leftrightarrow x=2\)
\(\Rightarrow k=-2\Rightarrow\) phương trình tiếp tuyến : \(y=-2x+7\)
b. Gọi d là đường thẳng đi qua A, có hệ số góc k : \(d:y=k\left(x-2\right)-1\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-2\right)-1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-2\right)-1\Leftrightarrow x=\pm\sqrt{2}\)
* \(x=\sqrt{2}\Rightarrow k=-2\left(3+2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3+2\sqrt{2}\right)x+11+8\sqrt{2}\)
* \(x=-\sqrt{2}\Rightarrow k=-2\left(3-2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3-2\sqrt{2}\right)x+11-8\sqrt{2}\)

Xét phương trình hoành độ giao điểm của đồ thị (C) và d :
\(\frac{2x+3}{x+2}=-2x+m\)\(\Leftrightarrow\begin{cases}x\ne-2\\2x^2+\left(6-m\right)x+3-2m=0\end{cases}\) (*)
Xét phương trình (*), ta có \(\Delta>0\), mọi \(m\in R\) và x=-2 không là nghiệm của (*) nên d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B với mọi m
Hệ số góc của tiếp tuyến tại A, tại B lần lượt là :
\(k_1=\frac{1}{\left(x_1+1\right)^2};k_2=\frac{1}{\left(x_2+1\right)^2}\) trong đó \(x_1,x_2\) là 2 nghiệm của phương trình (*)
Ta thấy :
\(k_1.k_2=\frac{1}{\left(x_1+1\right)^2.\left(x_2+1\right)^2}=\frac{1}{\left(x_1x_2+2x_1+2x_2+4\right)^2}=4\) (\(k_1>0;k_2>0\) )
Có \(P=\left(k_1\right)^{2014}+\left(k_2\right)^{2014}\ge2\sqrt{\left(k_1k_2\right)^{2014}}=2^{2015}\)
Do đó , Min \(P=2^{2015}\) đạt được khi và chỉ khi \(k_1=k_2\)
\(\Leftrightarrow\frac{1}{\left(x_1+2\right)^2}=\frac{1}{\left(x_2+2\right)^2}\Leftrightarrow\left(x_1+2\right)^2=\left(x_2+2\right)^2\)
Do \(x_1,x_2\) phân biệt nên ta có \(x_1+2=-x_2-2\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow m=-2\)
Vậy giá trị cần tìm là \(m=-2\)

Đặt \(A\left(a;a^3-3a^2+2\right);B\left(b;b^3-3b^2+2\right);a\ne b\)
Hệ số góc của tiếp tuyến với (C) tại A, B là :
\(k_A=y'\left(x_A\right)=3a^2-6a;k_B=y'\left(x_B\right)=3b^2-6b\)
Tiếp tuyến của (C) tại A và B song song với nhau khi và chỉ khi \(k_A=k_B\)
\(\Leftrightarrow3a^2-6a=3b^2-6b\Leftrightarrow\left(a-b\right)\left(a+b-2\right)=0\)
\(\Leftrightarrow b=2-a\)
Độ dài đoạn AB là :
\(AB=\sqrt{\left(a-b\right)^2+\left[a^3-b^3-3\left(a^2-b^2\right)\right]^2}\)
\(=\sqrt{\left(a-b\right)^2+\left(a-b\right)^2.\left[a^2+ab+b^2-3\left(a+b\right)\right]^2}\)
\(=\sqrt{4\left(a-1\right)^2+4\left(a-1\right)^2\left[\left(a-1\right)^2-3\right]^2}\)
Đăth \(\left(a-1\right)^2=t\) mà \(AB=4\sqrt{2}\Leftrightarrow t+t\left(1-3\right)^2=8\Leftrightarrow\left(t-4\right)\left(t^2-2t+2\right)=0\)
\(\Leftrightarrow t=4\Rightarrow\left[\begin{array}{nghiempt}a-1=2\\a-1=-2\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}a=3\\a=-1\end{array}\right.\)
* Với \(a=3\Rightarrow b=-1\Rightarrow A\left(3;2\right);B\left(-1;-2\right)\)
* Với \(a=1\Rightarrow b=3\Rightarrow A\left(-1;-2\right);B\left(3;2\right)\)
Vậy \(A\left(-1;-2\right);B\left(3;2\right)\) hoặc \(A\left(3;2\right);B\left(-1;-2\right)\)

Phương trình hoành độ giao điểm của \(\left(\Delta_m\right)\) và \(\left(C_m\right)\) được viết thành :
\(\left(x+1\right)\left(x^2-3mx+2m^2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-m\right)\left(x-2m\right)=0\)
\(\Rightarrow\) Giao điểm của \(\left(\Delta_m\right)\) và \(\left(C_m\right)\) gồm \(A\left(-1;-m-m^2\right);B\left(m;0\right)\) và \(C\left(2m;m^2\right)\), trong số đó, A là điểm duy nhất có hoành độ không đổi (khi m thay đổi)
Đặt \(f_m\left(x\right)=x^3-\left(3m-1\right)x^2+2m\left(m-1\right)x+m^2\)
Các tiếp tuyến của \(\left(C_m\right)\) tại B và C lần lượt là các đường thẳng :
\(\left(\Delta_B\right):y=f_m'\left(x_B\right)x+y_b-f_m'\left(x_B\right)x_B\)
\(\left(\Delta_C\right):y=f_m'\left(x_C\right)x+y_C-f_m'\left(x_C\right)x_C\)
Ta cần tìm m để B và C cùng khác A và \(\Delta_B\backslash\backslash\Delta_C\), tức là :
\(\begin{cases}x_B\ne x_A\\x_C\ne x_A\\f'_m\left(x_B\right)=f'_m\left(x_C\right)\\y_B-f'_m\left(x_B\right)x_B\ne y_C-f'_m\left(x_C\right)x_C\end{cases}\)\(\Leftrightarrow\begin{cases}m\ne-1\\m\ne-\frac{1}{2}\\-m^2=2m^2+2m\\m^3\ne-4m^3-3m^2\end{cases}\)
\(\Leftrightarrow m=-\frac{2}{3}\)

1.
Để ĐTHS có 2 tiệm cận thì \(m\ne-3\)
Khi đó:
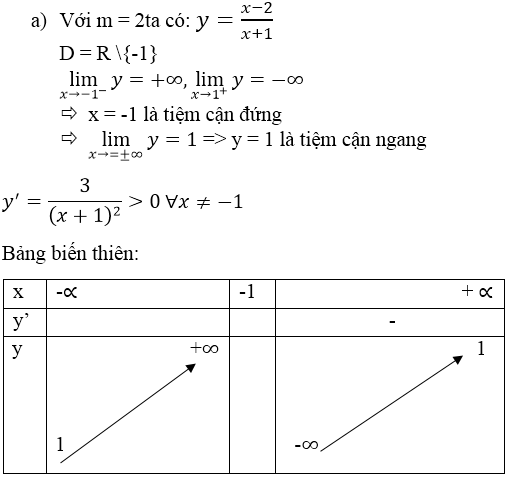
\(\lim\limits_{x\rightarrow\infty}\frac{mx-3}{x+1}=m\Rightarrow y=m\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow-1}\frac{mx-3}{x+1}=\infty\Rightarrow x=-1\) là tiệm cận đứng
Giao điểm 2 tiệm cận có tọa độ \(A\left(-1;m\right)\)
Để A thuộc \(y=x+3\Leftrightarrow m=-1+3\Rightarrow m=2\)
2.
\(\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{x-2}}{x^2-4}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow2}\frac{\sqrt{x-2}}{x^2-4}=\infty\Rightarrow x=2\) là 1 TCĐ
\(x=-2\) ko thuộc TXĐ nên ko phải là tiệm cận
Vậy ĐTHS có 2 tiệm cận
3.
Để ĐTHS có đúng 2 TCĐ \(\Leftrightarrow x^2-mx+5=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}6-m\ne0\\\Delta=m^2-20>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne6\\\left[{}\begin{matrix}m\ge2\sqrt{5}\\m\le-2\sqrt{5}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{5;-5\right\}\)
Đề bài sai hoặc đáp án sai
 ...">
...">


Đáp án D