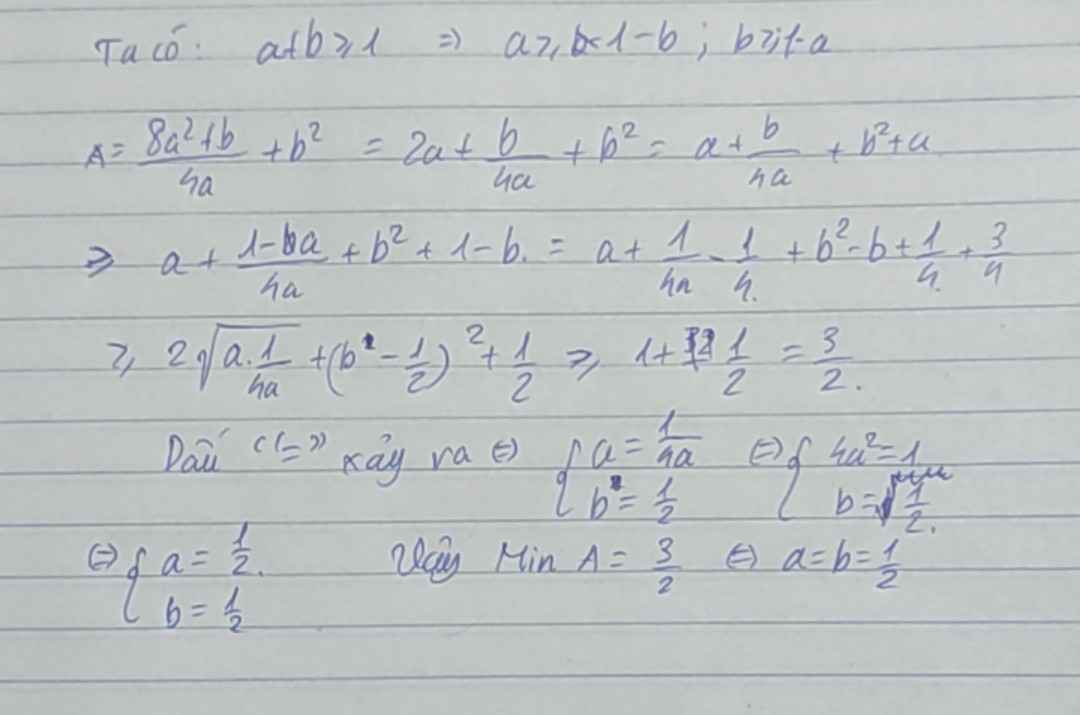Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét Q^2=(a^2+b^2)^2/(a-b)^2.Đặt a^2+b^2=x thì (a-b)^2=a^2+b^2-2ab=x-4.Do a>b nên x-4>0.
A^2=x^2/x-4=(x^2-16)/x-4+16/(x-4)=x+4+16/x-4=x-4+16/(x-4)+8>=8+8=16(dùng Cô-si cho 2 số)
suy ra A>=4.
Dấu =xảy ra khi x-4=16(x-4)>>>x-4=4>>>x=8>>>a-b=2 và a+b=2 căn 3 >>>tìm ra a và b
Xét Q^2=(a^2+b^2)^2/(a-b)^2.Đặt a^2+b^2=x thì (a-b)^2=a^2+b^2-2ab=x-4.Do a>b nên x-4>0.
A^2=x^2/x-4=(x^2-16)/x-4+16/(x-4)=x+4+16/x-4=x-4+16/(x-4)+8>=8+8=16(dùng Cô-si cho 2 số)
suy ra A>=4.
Dấu =xảy ra khi x-4=16(x-4)>>>x-4=4>>>x=8>>>a-b=2 và a+b=2 căn 3 >>>tìm ra a và b
k cho mk nha $_$

p = \(\frac{a^2+b^2-2ab+9}{a-b}\)
= (a-b) + \(\frac{9}{a-b}\)
= (\(\sqrt{a-b}\) - \(\frac{3}{\sqrt{a-b}}\))\(^2\) +6
p lớn nhất= 6 khi \(\sqrt{a-b}\)=\(\frac{3}{\sqrt{a-b}}\)
a- b = 3
mà ab = 4
giải pt bậc 2
có a=4, b=1 hoặc a= -1, b= -4

đặt \(t=a+b\) từ GT => \(3=t^2-ab\ge\frac{3}{4}t^2\)\(\Leftrightarrow\)\(-2\le t\le2\)
\(P=-4t^3-3t^2+18t+9=\hept{\begin{cases}\frac{-1}{4}\left(2t+3\right)^2\left(4t-9\right)-\frac{45}{4}\ge\frac{-45}{4}\left(dungvoit\le2\right)\\-\left(t-1\right)^2\left(4t+11\right)+20\le20\left(dungvoit\ge-2\right)\end{cases}}\)
\(P_{min}=\frac{-45}{4}\) tại
\(\hept{\begin{cases}a^2+b^2+ab=3\\a+b=\frac{-3}{2}\end{cases}}\Leftrightarrow\left(a;b\right)=\left\{\left(\frac{-3-\sqrt{21}}{4};\frac{-3+\sqrt{21}}{4}\right);\left(\frac{-3+\sqrt{21}}{4};\frac{-3-\sqrt{21}}{4}\right)\right\}\)
\(P_{max}=20\) tại \(\hept{\begin{cases}a^2+b^2+ab=3\\a+b=1\end{cases}}\Leftrightarrow\left(a;b\right)=\left\{\left(2;-1\right);\left(-1;2\right)\right\}\)

\(2a^2+\frac{1}{a^2}+\frac{b^2}{4}=4\Leftrightarrow\left(a^2+\frac{1}{a^2}-2\right)+\left(a^2+\frac{b^2}{4}-ab\right)=4-ab-2\)
\(\Leftrightarrow\left(a-\frac{1}{a}\right)^2+\left(a-\frac{b}{2}\right)^2=2-ab\)
\(VF=2-ab=\left(a-\frac{1}{a}\right)^2+\left(b-\frac{b}{2}\right)^2\ge0\)
Hay \(ab\le2\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=\frac{1}{a}\\b=\frac{b}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(a;b\right)=\left(1;\frac{1}{2}\right)\\\left(a;b\right)=\left(-1;-\frac{1}{2}\right)\end{cases}}\)

\(a+\frac{1}{b}\le1=>ab+1\le b\)
\(b\le ab+1\ge2\sqrt{ab}=>\sqrt{b}\ge2\sqrt{a}=>\frac{b}{a}\ge4\)
\(T=\frac{ab}{a^2+b^2}=\frac{1}{\frac{a}{b}+\frac{b}{a}}=\frac{1}{\frac{a}{b}+\frac{b}{16a}+\frac{15b}{16a}}\)
áp dụng cô si
\(\frac{a}{b}+\frac{b}{16a}\ge2\sqrt{\frac{ab}{16ab}}=\frac{1}{2}=>T\le\frac{1}{\frac{1}{2}+\frac{15}{16}.4}=\frac{4}{17}\)
\(=>MaxT=\frac{4}{17}\)
dấu = xảy ra khi
\(b=4a;\frac{a}{b}=\frac{b}{16a};ab=1\)
\(=>\hept{\begin{cases}4a^2=1\\b=4a\end{cases}=>\hept{\begin{cases}a=\frac{1}{2}\\b=2\end{cases}}}\)

GT => (a+1)(b+1)(c+1)=(a+1)+(b+1)+(c+1)
Đặt \(\frac{1}{a+1}=x,\frac{1}{1+b}=y,\frac{1}{c+1}=z\), ta cần tìm min của\(\frac{x}{x^2+1}+\frac{y}{y^2+1}+\frac{z}{z^2+1}\)với xy+yz+zx=1
\(\Leftrightarrow\frac{x\left(y+z\right)+y\left(z+x\right)+z\left(x+y\right)}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\Leftrightarrow\frac{2}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\)Mà (x+y)(y+z)(z+x) >= 8/9 (x+y+z)(xy+yz+xz) >= \(\frac{8\sqrt{3}}{9}\) nên \(M\)=< \(\frac{3\sqrt{3}}{4}\),dấu bằng xảy ra khi a=b=c=\(\sqrt{3}-1\)
Theo giả thiết, ta có: \(abc+ab+bc+ca=2\)
\(\Leftrightarrow abc+ab+bc+ca+a+b+c+1=a+b+c+3\)
\(\Leftrightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)=\left(a+1\right)+\left(b+1\right)+\left(c+1\right)\)
\(\Leftrightarrow\frac{1}{\left(a+1\right)\left(b+1\right)}+\frac{1}{\left(b+1\right)\left(c+1\right)}+\frac{1}{\left(c+1\right)\left(a+1\right)}=1\)
Đặt \(\left(a+1;b+1;c+1\right)\rightarrow\left(\frac{\sqrt{3}}{x};\frac{\sqrt{3}}{y};\frac{\sqrt{3}}{z}\right)\). Khi đó giả thiết bài toán được viết lại thành xy + yz + zx = 3
Ta có: \(M=\Sigma_{cyc}\frac{a+1}{a^2+2a+2}=\Sigma_{cyc}\frac{a+1}{\left(a+1\right)^2+1}\)\(=\Sigma_{cyc}\frac{1}{a+1+\frac{1}{a+1}}=\Sigma_{cyc}\frac{1}{\frac{\sqrt{3}}{x}+\frac{x}{\sqrt{3}}}\)
\(=\sqrt{3}\left(\frac{x}{x^2+3}+\frac{y}{y^2+3}+\frac{z}{z^2+3}\right)\)
\(=\sqrt{3}\text{}\Sigma_{cyc}\left(\frac{x}{x^2+xy+yz+zx}\right)=\sqrt{3}\Sigma_{cyc}\frac{x}{\left(x+y\right)\left(x+z\right)}\)
\(\le\frac{\sqrt{3}}{4}\Sigma_{cyc}\left(\frac{x}{x+y}+\frac{x}{x+z}\right)=\frac{3\sqrt{3}}{4}\)
Đẳng thức xảy ra khi \(x=y=z=1\)hay \(a=b=c=\sqrt{3}-1\)